Category Archive

You are currently browsing the category archive for the ‘Problem of the Week (POW)’ category.

Solution to POW-13: Highly coincidental!

July 22, 2009 in Algebraic Geometry, Problem of the Week (POW) | Tags: elliptic curves, pascal's mystic hexagon | by Todd Trimble | 18 comments

Huh — no solutions to POW-13 came in! I guess I was surprised by that.

Ah well, that’s okay. The problem wasn’t exactly trivial; there are some fairly deep and interesting things going on in that problem that I’d like to share now. First off, let me say that the problem comes from The Unapologetic Mathematician, the blog written by John Armstrong, who posted the problem back in March this year. He in turn had gotten the problem from Noam Elkies, who kindly responded to some email I wrote and had some pretty insightful things to say.

In lieu of a reader solution, I’ll give John’s solution first, and then mine, and then touch on some of the things Noam related in his emails. But before we do so, let me paraphrase what John wrote at the end of his post:

Here’s a non-example. Pick $m$ points $(1, 0), (2, 0), (3, 0)$ and so on up to $(m, 0)$ . Pick $n$ points $(1, 1)$ , $(2, 1)$ , $(3, 1)$ , and so on up to $(n, 1)$ . In this case we have $m+n-1$ blocking points at $(1, \frac1{2})$ , $(\frac{3}{2}, \frac1{2})$ , and so on by half-integers up to $(\frac{m+n}{2}, \frac1{2})$ . Of course this solution doesn’t count because the first $m$ points lie on a line as do the $n$ points that follow, which violates the collinearity condition of the problem.

Here’s a picture of that scenario when $m = n = 3$ :

pappusa

Does this configuration remind you of anything? Did somebody say “Pappus’s theorem“? Good. Hold that thought please.

Okay, in the non-example the first $m+n$ points were on two lines, which is disallowed. Now the two lines here, $y = 0$ and $y = 1$ , form a degenerate conic $y^2 - y = 0$ . Thinking in good algebraic geometry fashion, perhaps we can modify the non-solution by replacing the degenerate conic by an honest (smooth) nondegenerate conic, like an ellipse or something, so that at most two of the $m+n$ points are on any given line. This should put one in the mood for our first solution.

John Armstrong writes: Basically, I took the non-example and imagined bending back the two lines to satisfy the collinearity (pair-of-lines = degenerate conic, so non-example is degenerate example). The obvious pair of curves to use is the two branches of a hyperbola. But hyperbolas can be hard to work with, so I decided to do a projective transformation to turn it into a parabola.

So let’s consider points on a parabola. The points $(-i, i^2)$ and $(j, j^2)$ are connected by a line of slope

$\displaystyle \frac{j^2 - i^2}{j + i} = j - i$

The line itself is $y = (j-i)x + i j$ . Which has the obvious $y$ -intercept $(0, i j)$ . Now we need to pick a lot of $i$ and $j$ values to get repeated products. Place $m$ points at $(-1, 1)$ , $(-2, 4)$ , $(-4, 16)$ , $(-8, 64)$ , and so on above the negative powers of two. Place $n$ points at $(1, 1)$ , $(2, 4)$ , $(4, 16)$ , $(8, 64)$ , and so on above the positive powers of two. The blocking points are then at $(0, 1)$ , $(0, 2)$ , $(0, 4)$ , $(0, 8)$ , and so on up the $y$ -axis by powers of two. Presto! $\Box$

Very nice. My own solution was less explicit in the sense that I didn’t actually write down coordinates of points, but gave instead a general recipe which relies instead on the geometry of conics, in fact on a generalization of Pappus’s theorem known to me as “Pascal’s mystic hexagon“. I first learned about this from a wonderful book:

C. Herbert Clemens, A Scrapbook of Complex Curve Theory (2nd Edition), Graduate Studies in Mathematics 55, AMS (2002).

Pascal’s Mystic Hexagon, version A: Consider any hexagon inscribed in a conic, with vertices marked $x_1, x_2, x_3, y_1, y_2, y_3$ . For $i \neq j$ , mark the intersection of the lines $\overline{x_i y_j} \cap \overline{x_j y_i}$ by $z_{i+j-1}$ . Then $z_2, z_3, z_4$ are collinear. (The reason for the strange indexing will be clear in a moment.)

mystic1

Pascal’s Mystic Hexagon, version B: Consider any pentagon inscribed in a conic $C$ , with vertices marked $x_1, x_2, x_3, y_1, y_2$ . Choose any line $L$ through $z_2 = \overline{x_1 y_2} \cap \overline{y_1 x_2}$ , and define $z_3 = L \cap \overline{y_1 x_3}$ and $z_4 = L \cap \overline{y_2 x_3}$ . Then the intersection $y_3 := \overline{x_1 z_3} \cap \overline{x_2 z_4}$ is the sixth point of a hexagon inscribed in $C$ .

The following solution uses version B.

Solution by Todd and Vishal: For the sake of explicitness, let the conic $C$ be a circle $x^2 + y^2 = 1$ and let the line (segment) $L$ be the diameter along $y = 0$ . Choose two points $x_1, x_2$ on $C$ above $L$ and a point $y_1$ on $C$ below $L$ . The remaining points are determined recursively by a zig-zag procedure, where at each stage $x_{n+1}$ is the intersection $C \cap \overline{y_1 z_{n+1}}$ , where $z_{2n} = L \cap \overline{x_{n+1} y_n}$ , where $y_{n+1} = C \cap \overline{x_1 z_{n+1}}$ , and $z_{2n+1} = L \cap \overline{x_{n+1} y_{n+1}}$ . We will show the blocking condition is satisfied: for all $i, j$ , the point $z_{i+j-1}$ is on the line $\overline{x_i y_j}$ .

To get started, notice that the blocking condition is trivially satisfied up to the point where we construct $z_1, z_2, y_2, z_3, x_3, z_4$ . Mystic Hexagon B ensures that $y_3$ , as defined above, is blocked from $x_1$ by $z_3$ and from $x_2$ by $z_4$ . Then define $z_5$ as above. So far the blocking condition is satisfied.

mystic2a

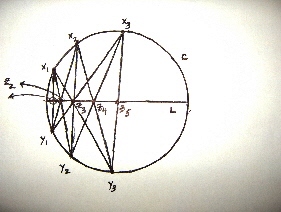
Suppose the blocking condition is satisfied for the points $x_1, \ldots, x_n, y_1, \ldots, y_n, z_1, \ldots, z_{2n-1}$ . Define $x_{n+1} = C \cap \overline{y_1 z_{n+1}}$ , as above. Then Mystic Hexagon B, applied to the pentagon consisting of points $y_1, y_2, y_3, x_{n-1}, x_n$ , shows that $x_{n+1}$ is blocked from $y_1$ by $z_{n+1}$ and from $y_2$ by $z_{n+2}$ .

This shows that $x_{n+1}$ could have been defined to be $C \cap \overline{y_2 z_{n+2}}$ . Then Mystic Hexagon B, applied to the pentagon $y_2, y_3, y_4, x_{n-1}, x_n$ , shows that $x_{n+1}$ is blocked from $y_2$ by $z_{n+2}$ and from $y_3$ by $z_{n+3}$ . This shows $x_{n+1}$ could have been defined to be $C \cap \overline{y_3 z_{n+3}}$ .

And so on up the inductive ladder: for $2 \leq i \leq n-1$ , defining $x_{n+1} = C \cap \overline{y_{i-1} z_{n+i-1}}$ , Hexagon B applied to the pentagon $y_{i-1}, y_i, y_{i+1}, x_{n-1}, x_n$ shows that $x_{n+1}$ could have been defined to be $C \cap \overline{y_i z_{n+i}}$ . This shows the blocking condition is satisfied for $1 \leq i \leq n+1$ , $1 \leq j \leq n-1$ . We block $x_{n+1}$ from $y_n$ by defining $z_{2n}$ as above, to extend up to $j = n$ .

Then, as prescribed above, we define $y_{n+1} = C \cap \overline{x_1 z_{n+1}}$ , and repeat the preceding argument mutatis mutandis (interchanging $x$ ‘s and $y$ ‘s), to obtain the blocking conditions up to $1 \leq i \leq n+1$ , $1 \leq j \leq n+1$ . This completes the proof. $\Box$

What this argument shows (with Hexagon B doing all the heavy lifting) is that no cleverness whatsoever is required to construct the desired points: starting with any nondegenerate conic $C$ , any secant line $L$ , and any three initial points $x_1, x_2, y_1$ on $C$ to get started (with $x_1, x_2$ ‘s on one side of $L$ and $y_1$ on the other), the whole construction is completely forced and works no matter what!

Which may lead one to ask: what is behind this “miracle” called Pascal’s Mystic Hexagon? Actually, not that much! Let me give a seat-of-the-pants argument for why one might expect it to hold, and then give a somewhat more respectable argument.

Define a planar cubic to be the locus $P(x, y) = 0$ of any degree 3 polynomial $P$ in two variables. (We should actually be doing this as projective geometry, so I ought to write $P(x, y, z) = 0$ where $P$ is homogeneous of degree 3, but I think I’ll skip that.) For example, the union of three distinct lines is a cubic where $P$ is a product of three degree 1 polynomials. What is the dimension of the space of planar cubics? A cubic polynomial $P(x, y)$ ,

$a_0 + a_1 x + a_2 y + a_3 x^2 + a_4 x y + a_5 y^2 + a_6 x^3 + a_7 x^2 y + a_8 x y^2 + a_9 y^3,$

has 10 coefficients. But the equation $P(x, y) = 0$ is equivalent to the equation $\lambda P(x, y) = 0$ for any nonzero scalar $\lambda$ ; modding out by scalars, there are 9 degrees of freedom in the space of cubics. What is the dimension of the space of cubics passing through a given point $(x, y) = (a, b)$ ? The condition $P(a, b) = 0$ gives one linear equation on the coefficients $a_0, \ldots, a_9$ , so we cut down a degree of freedom, and the dimension would be 8. Similarly, if we ask for the dimension of cubics passing through 8 given points, we get a system of eight linear equations, and we cut down by eight degrees of freedom: in general, the space of cubics through 8 points is “expected” to be (is “almost always”) 1-dimensional, in fact, a (projective) line.

In the configuration for Pascal’s Mystic Hexagon, version A

mystic1

we see three cubics passing through the 8 points $x_1, x_2, x_3, y_1, y_2, y_3, z_2, z_3$ , namely:

$A = \overline{x_1 y_2} \cup \overline{x_2 y_3} \cup \overline{x_3 y_1}$
$B = \overline{x_2 y_1} \cup \overline{x_3 y_2} \cup \overline{x_1 y_3}$
$C \cup L$ where the conic $C$ is defined by a degree 2 polynomial

Since we expect that the space of cubics through these eight points is a line, we should have a linear relationship between the cubic polynomials $P, Q, R$ used respectively to define $A, B$ , and $C \cup L$ above, hence we would get

$\lambda P(x, y) + \mu Q(x, y) = R(x, y)$

for some scalars $\lambda, \mu$ . Thus, if a ninth point $z_4 = (a, b)$ is in $A$ and $B$ , so that $P(a, b) = Q(a, b) = 0$ , then $R(a, b) = 0$ . Thus $z_4$ lies in $C \cup L$ as well, and if $z_4$ isn’t on $C$ , it must be on the line $L$ . Thus, “generically” we expect $z_2, z_3, z_4$ to be collinear, whence Hexagon A.

This rough argument isn’t too far removed from a slightly more rigorous one. There’s a general result in projective algebraic geometry called Bézout’s theorem, which says that a degree $m$ planar curve and a degree $n$ planar curve either intersect in $m n$ points (if you count them right, “with multiplicity”) or they have a whole curve component in common. (Fine print: to make this generally true, you have to work in the projective plane, and you have to work over an algebraically closed field.) A much weaker result which removes all the fine print is that a degree $m$ curve and a degree $n$ curve either have a curve component in common, or they intersect in at most $m n$ points. In particular, in the notation above, the cubics $A$ and $B$ intersect in 9 points, 6 of which are on the conic $C$ . Pick a seventh point $(a, b)$ on $C$ , away from those six, and let $\lambda = Q(a, b)$ and $\mu = -P(a, b)$ . Then we see that the locus of the degree 3 polynomial

$T(x, y) = \lambda P(x, y) + \mu Q(a, b) = 0$

intersects the degree 2 conic $C$ in at least 7 points (namely, $x_1, x_2, x_3, y_1, y_2, y_3$ and $(a, b)$ ), greater than the expected number $3 \cdot 2$ , which is impossible unless the loci of $T$ and $C$ have a component in common. But the conic $C$ has just one component — itself — so one can conclude that its defining degree 2 polynomial (I’ll call it $C(x, y)$ ) must divide $T$ . Then we have

$T(x, y) = \lambda P(x, y) + \mu Q(x, y) = C(x, y)L(x, y)$

for some degree 1 polynomial $L$ , so the last three of the nine points of intersection $A \cap B$ , which are zeroes of $P$ and $Q$ , must be zeroes of the linear polynomial $L$ , and hence are collinear. Thus we obtain Pascal’s Mystic Hexagon, version A. $\Box$

It’s clear then that what makes the Mystic Hexagon tick has something to do with the geometry of cubic curves. With that in mind, I’m now going to kick the discussion up a notch, and relate a third rather more sophisticated construction on cubics which basically subsumes the first two constructions. It has to do with so-called “elliptic curves“.

Officially, an elliptic curve is a smooth projective (irreducible) cubic “curve” over the complex numbers. I put “curve” in quotes because while it is defined by an equation $P(x, y) = 0$ where $P$ is a polynomial of degree 3, the coefficients of $P$ are complex numbers as are the solutions to this equation. We say “curve” in the sense that locally it is like a “line”, but this is the complex line $\mathbb{C}$ we’re talking about, so from our real number perspective it is two-dimensional — it actually looks more like a surface. Indeed, an elliptic curve is an example of a Riemann surface. It would take me way too far afield to give explanations, but when you study these things, you find that elliptic curves are Riemann surfaces of genus 1. In more down-to-earth terms, this means they are tori (toruses), or doughnut-shaped as surfaces. Topologically, such tori or doughnuts are cartesian products of two circles.

Now a circle or 1-dimensional sphere $S^1$ carries a continuous (abelian) group structure, if we think of it as the set of complex numbers $\{z: |z| = 1\}$ of norm 1, where the group operation is complex multiplication. A torus $S^1 \times S^1$ also carries a group structure, obtained by multiplying in each of the two components. Thus, given what we have said, an elliptic curve also carries a continuous group structure. But it’s actually much better than that: one can define a group structure on a smooth complex cubic $C$ (in the complex plane $\mathbb{C}^2$ , or rather the projective complex plane $P^2(\mathbb{C})$ ) not just by continuous operations, but by polynomially defined operations, and the definition of the group law is just incredibly elegant as a piece of geometry. Writing the group multiplication as addition, it says that if $a, b, c$ are points on $C$ , then

$a + b = -c \qquad (a + b + c = 0)$

if $a, b, c$ are collinear. [To be precise, one must select a point 0 on $C$ to serve as identity, and this point must be one of the nine inflection points of $C$ . When $a$ and $b$ coincide (are “infinitesimally close”), the line through $a$ and $b$ is taken to be tangent to $C$ ; when $a, b, c$ coincide, this is a line of inflection.]

This is rather an interesting thing to prove, that this prescription actually satisfies the axioms for an abelian group. The hardest part is proving associativity, but this turns out to be not unlike what we did for Pascal’s Mystic Hexagon: basically it’s an application of Bézout’s theorem again. (In algebraic geometry texts, such as Hartshorne’s famous book, the discussion of this point can be far more sophisticated, largely because one can and does define elliptic curves as certain abstract 1-dimensional varieties or schemes which have no presupposed extrinsic embeddings as cubic curves in the plane, and there the goal is to understand the operations intrinsically.)

In the special case where $C$ is defined by a cubic polynomial with real coefficients, we can look at the locus of real solutions (or “real points”), and it turns out that this prescription for the group law still works on the real locus, in particular is still well-defined. (Basically for the same reason that if you have two real numbers $a, b$ which are solutions to a real cubic equation $p(x) = 0$ , then there is also a third real solution $c$ .) There is still an identity element, which will be an inflection point of the cubic.

Okay, here is a third solution to the problem, lifted from one of Noam Elkies’ emails. (The original formulation of the problem spoke in terms of $r$ “red” points (instead of my $x_1, \ldots, x_m$ ), $b$ “blue” points (instead of my $y_1, \ldots, y_n$ ), and “blocking” points which play the role of my $z_1, \ldots, z_{m+n-1}$ .) The addition referred to is the addition law on an elliptic curve. I’ve taken the liberty of paraphrasing a bit.

“Choose points $B, R$ on the real points of an elliptic curve such that $-(B+R)$ is in-between $B$ and $R$ . Then set

red points: $R + i P$ , $0 \leq i \leq r-1$
blue points: $B + j P$ , $1 \leq j \leq b-1$
blocking points: $-(R+B+kP)$ , $0 \leq k \leq r+b-2$

where $P$ is a real point on the elliptic curve very close to the identity. The pair $R + i P$ , $B + j P$ is blocked by $-(R + B + (i + j)P$ , because these three points are collinear, and the smallness of P guarantees that the blocking point is actually between the red point and blue point, by continuity.”

Well, well. That’s awfully elegant. (According to Noam’s email, it came out of a three-way conversation between Roger Alperin, Joe Buhler, and Adam Chalcraft. Edit: Joe Buhler informs me in email that Joel Rosenberg’s name should be added. More at the end of this post.) Noam had given his own slick solution where again the red and blue points sit on a conic and the blocking points lie on a line not tangent to the conic, and he observed that his configuration was a degenerate cubic, leading him to surmise that his example could in a sense be seen as a special case of theirs.

How’s that? The last solution took place on a smooth (nondegenerate) cubic, so the degenerate cubic = conic+line examples could not, literally speaking, be special cases. Can the degenerate examples be seen in terms of algebraic group structures based on collinearity?

The answer is: yes! As you slide around in the space of planar cubics, nondegenerate cubics (the generic or typical case) can converge to cubics which are degenerate in varying degrees (including the case of three lines, or even a triple line), but the group laws on nondegenerate cubics based on collinearity converge to group laws, even in degenerate cases! (I hadn’t realized that.) You just have to be careful and throw away the singular points of the degenerate cubic, but otherwise you can basically still use the definition of the group law based on collineation, although it gets a little tricky saying exactly how you’re supposed to add points on a line component, such as the line of conic+line.

So let me give an example of how it works. It seems convenient for this purpose to use John Armstrong’s model which is based on the parabola+line, specifically the locus of $(y - x^2)x = 0$ . The singular points of its projective completion are at $(0, 0)$ and the point where the $y$ -axis meets the line at infinity. After throwing those away, what remains is a disjoint union of four pieces: right half of parabola, left half of parabola, positive $y$ -axis, negative $y$ -axis.

We can maybe guess that since $a + b + c = 0$ implies $a, b, c$ collinear, that the two pieces of the $y$ -axis form a subgroup for the group law we are after (also, these two pieces together should suggest the two halves of the multiplicative group of nonzero reals $\mathbb{R}^*$ , but don’t jump to conclusions how this works!). If so, then we notice that if $a$ and $b$ lie on the parabola, then the line between them intersects the $y$ -axis at a point $c$ , so then the parabolic part would not be closed under multiplication.

One is then led to consider that the group structure of this cubic overall is isomorphic to the group $\{-1, 1\} \times \mathbb{R}^*$ , with the linear part identified somehow with the subgroup $\{1\} \times \mathbb{R}^*$ , and the parabolic part with $\{-1\} \times \mathbb{R}^*$ .

I claim that the abelian group structure on the punctured $y$ -axis should be defined by

$(0, x) + (0, y) := (0, - x y)$

so that the identity element on the cubic is $(0, -1)$ , and the inverse of $(0, x)$ is $(0, 1/x)$ . The remainder of the abelian group structure on the cubic is defined as follows:

$(s, s^2) + (t, t^2) := (0, -1/(s t))$

$(0, x) + (s, s^2) := (-s/x, s^2/x^2)$

Undoubtedly this group law looks a bit strange! So let’s do a spot check. Suppose $(0, a)$ , $(s, s^2)$ , and $(t, t^2)$ are collinear. Then it is easily checked that $a = -s t$ , and each of the two equations

$(0, a) + (s, s^2) = (t^{-1}, t^{-2}) = -(t, t^2)$

$(s, s^2) + (t, t^2) = (0, 1/a) = -(0, a)$

is correct according to the group law, so the three collinear points do add to the identity and everything checks out.

All right, let’s retrieve John’s example as a special case. Take $R = (1, 1)$ as a red point, $B = (-1, 1)$ as a blue point, and $-(B + R) = (0, 1)$ as blocking point. Take a point $P$ “sufficiently close” to the identity, say $(0, -1/2)$ . Then

$R + i P = (1, 1) + (0, -1/2^i) = (2^i, 2^{2i})$

$B + j P = (-1, 1) + (0, -1/2^j) = (-2^j, 2^{2j})$

which was John’s solution.

Another long post from yours truly. I was sorry no solutions came from our readers, but if you’d like another problem to chew on, here’s a really neat one I saw just the other day. Feel free to discuss in comments!

Exercise: Given a point on a circle, show how to draw a tangent to the point using ruler only, no compass. Hint: use a mystic hexagon where two of the points are “infinitesimally close”.

Added July 25: As edited in above, Joel Rosenberg also had a hand in the elliptic curves solution, playing an instrumental role in establishing some of the conjectures, such as that $r + b - 1$ is the minimal number of blocking points under certain assumptions, and (what is very nice) that the elliptic curves solution is the most general solution under certain assumptions. I thank Joe Buhler for transmitting this information.

POW-13: Highly coincidental!

July 10, 2009 in Problem of the Week (POW) | Tags: collinearity, linear coincidence | by Todd Trimble | 8 comments

It’s been an awfully long time since I’ve posted anything; time to finally break the silence.

This problem appeared elsewhere on the internet some months ago; some of you may have already seen it. I don’t want to say right away where I saw it, because there was some commentary which included some rough hints which I don’t want to give, but I’ll be sure to give credit when the solution is published. I’ll bet some of you will be able to find a solution, and will agree it’s quite cute. Here it is:

Given integers $m, n \geq 1$ , show that it is possible to construct a set of $m + n$ points in the plane, let’s say $x_1, \ldots, x_m, y_1, \ldots, y_n$ , so that no three points of the set are collinear, and for which there exist points $z_1, z_2, \ldots, z_{m+n-1}$ , all lying on a straight line, and arranged so that on the line between any $x_i$ and any $y_j$ , some $z_k$ lies between them.

So no $x_i$ can “see” any $y_j$ , because there’s always some $z_k$ blocking the view. As the proposer observed, the problem would be easy if we had $m n$ $z$ ‘s to play with, one for each pair $(x_i, y_j)$ . But here there are only $m+ n-1$ $z$ ‘s, so some of them will have to do more than their fair share, blocking the view between quite a few $(x, y)$ -pairs simultaneously. Thus, you have to arrange the $x$ ‘s and $y$ ‘s so that a lot of the lines between them will be coincident at a point $z$ , and subject to the constraint I italicized above.

Please submit solutions to topological[dot]musings[At]gmail[dot]com by Friday, July 17, 11:59 pm (UTC); do not submit solutions in Comments. Everyone with a correct solution will be inducted into our Hall of Fame! We look forward to your response.

Solution to POW-12: A graph coloring problem

January 4, 2009 in Problem of the Week (POW), Puzzles | by Todd Trimble | 22 comments

The solutions are in! This problem of the week was interesting for me: the usual pattern has been that I pose problems that I’ve solved myself at some point in the past, giving me a kind of “inside edge” on understanding the solutions that come in. But, as I said in POW-12, the difference this time is that the solution I knew of came from someone else (Arin Chaudhuri). What was interesting for me — and given the circumstances, it was probably inevitable — is that some of the solutions we received forced me to make contact with some mathematics I’d only heard about but never studied. Let me get to that in a minute.

Another interesting thing for me — speaking now with my category theorist’s hat on — is how utterly simple and conceptual Arin’s proof was! I was pleased to see that regular problem solver Philipp Lampe also spotted it. Wait for it…

Solution I by Philipp Lampe, University of Bonn: The answer is 8.

Among the eight neighbors of an arbitrary vertex, all colors of an admissible coloring must occur. Thus, 8 is an upper bound for the maximum number of colors one can use. We have to show that there is an admissible coloring with eight colors.

The vertices of the 8-dimensional cube may be represented by vectors $(a_1, a_2, \ldots, a_8)$ with $a_i$ in $\{0,1\}$ , in other words as vectors in $\mathbb{F}_{2}^8$ , the 8-dimensional vector space over the field $\mathbb{F}_2 = \{0, 1\}$ with two elements (i.e., the integers modulo 2). Two such vectors $u, v$ are neighbors iff their coordinate vectors differ in exactly one place, in other words if $u = v + e_i$ considered modulo 2, where $e_i$ is one of the eight standard basis elements (with $i$ -th coordinate 1, and the other coordinates 0).

Now let our “colors” be the 8 elements $x_1, x_2, \ldots, x_8$ of $\mathbb{F}_{2}^3$ , the 3-dimensional vector space over $\mathbb{F}_2$ . Let the vertex “coloring”

$C: \mathbb{F}_{2}^8 \to \mathbb{F}_{2}^3$

be the unique $\mathbb{F}_2$ -linear map such that $C(e_i) = x_i$ ; that is, define the color of a vertex/vector by

$\displaystyle C\left(a_1,\ldots, a_8\right) = \sum_{i=1}^{8} a_i x_i$

Now, if $v$ is any vector, the colors of its neighbors are $C(v + e_i) = C(v) + C(e_i) = C(v) + x_i$ . The colors of these neighbors are all distinct since the $x_i$ are distinct. Hence all 8 colors are represented among the colors of the neighbors of any given vertex $v$ , QED.

What I love about this solution it is how natural it is. I’ll say a little more about this in remarks below.

But I also learned a thing or two by studying the next solution. It relies on the theory of Hamming codes, with which I was not conversant. Up to some small edits, here is exactly what Sune Jakobsen submitted:

Solution II by Sune Jakobsen (first-year student), University of Copenhagen: Since each vertex only has 8 neighbors, the answer cannot be greater that 8.

Now we construct such a coloring with 8 colors. An 8-dimensional cube can be represented by the graph with vertices in $\{0, 1\}^8$ , and with an edge between them iff the Hamming distance between them is 1. We color a vertex with color 8 if the seven first bits in the vertex is a “correct” Hamming message (cf. Hamming code (7,4)), and color it in color $i$ if the first seven bits give a correct Hamming message upon changing bit $i$ . This is a well-defined coloring, since each element in $\{0, 1\}^7$ is either a correct Hamming message, or is Hamming distance 1 away to exactly one correct Hamming message.

It remains to show that no vertex is neighbor to two vertices of the same color. The Hamming distance between these two vertices is 2, thus the Hamming distance between the first 7 bits of two neighbors must be 1 or 2. If two neighbors had the same color $i$ , then by definition one would get two correct Hamming messages by changing bit $i$ in both of them, and the Hamming distance between these messages would be the same as before — either 1 or 2. But the distance between any two correct Hamming messages is at least 3. Contradiction.

Remarks:

1. Let me give a little background to Sune’s solution. Mathematically, the Hamming code called “(7, 4)” is the image of injective linear map

$G: \mathbb{F}_{2}^4 \to \mathbb{F}_{2}^7$

given by the $7 \times 4$ matrix

1101
1011
1000
0111
0100
0010
0001

The Hamming code is what is known as an “error-correcting code”. Imagine that you want to send a 4-bit message (each bit being a 0 or 1) down a transmission line, but that due to noise in the line, there is the possibility of a bit being flipped and the wrong message being received. What can you do to help ensure that the intended message is received?

The answer is to add some “parity check bits” to the message. In the code (7, 4), one adds in three parity checks, so that the transmitted message is 7 bits long. What one does is apply the matrix $G$ to the 4-vector, to get a 7-vector (remember we’re working modulo 2), and this 7-vector is sent down the line. Assuming only a moderate amount of noise in the transmission line, perhaps the 7-bit message will remain intact or perhaps a single bit will be flipped, more rarely two bits will be flipped (and we’ll assume the event that more than two are flipped has negligible probability). Now, the Hamming encoding $G$ is rigged up so that if the 7-bit vector is received as sent, then the parity checks will report 0 errors. If the parity checks report an error, they report precisely where the error occurred if the received vector was off by one bit. (If two flips occurred, then the receiver can still detect from the parity checks that an error occurred. The parity checks can never detect how many bits were flipped, but if the receiver assumes correctly that just one bit got flipped, he can restore the intended message with accuracy. If three or more got flipped, then the receiver got the wrong message, but he would never know it if the parity checks reported back 0 errors.)

How does this work? By having the receiver apply a parity-check matrix $H$ to the received message, given by the $3 \times 7$ matrix

1010101
0110011
0001111

In the first place, $HG = 0$ , and so if the message received belongs to the image of $G$ (is a “correct Hamming message” in the terminology of Solution II), which will indeed be the case if there were no errors in the transmission, then $H$ applied to the message will produce the zero vector. In the case where one bit got flipped in the transmission, $H$ applied to the received vector will return a nonzero 3-vector, but the beauty of the Hamming code is that the 3-vector will spell out in binary the bit the error occurred (for example, if the output vector is $(0 1 1)^t$ , then error occurred in the bit with binary number 011, that is bit 3). In that case, the receiver flips that bit to restore the original message. In these two cases, the original 4 bits are then read off as the 3rd, 5th, 6th, and 7th coordinates of the (possibly corrected) 7-vector.

By the way, Sune reminded us that Hamming codes also came up in a post by Greg Muller over at The Everything Seminar, who used the existence of a Hamming code in every dimension $2^k - 1$ to solve general hat-guessing puzzles.

2. Within minutes of posting the original problem, we received a message from David Eppstein, who reported that the solution of 8 colors is essentially contained in a paper he coauthored with T. Givaris (page 4); his solution is close in spirit to Sune’s.

Arin Chaudhuri also surmised the connection to Hamming codes, and mentions that the problem (in a slightly different formulation) originally came from a friend of a friend, who blogs about a number of related problems on this page. Presumably the author had things like error-correcting codes in mind.

3. Sune and David noted that their solutions generalize to show that on the $2^k$ -dimensional cube (for any $k$ ), it is possible to color the vertices with $2^k$ colors (the maximum number possible) so that all of the colors show up as colors of the neighbors of any given vertex.

This is very easy to see by adapting Philipp’s method. Indeed, for each $k$ just take the color set to be the $\mathbb{F}_2$ -vector space $S = \mathbb{F}_{2}^k$ . The set of vertices of the $2^k$ -dimensional cube may identified with the $\mathbb{F}_2$ -vector space $V(S)$ generated by the set $S$ (as basis), and the desired coloring is then just the $\mathbb{F}_2$ -linear map $C: V(S) \to S$ that extends the identity function on $S$ . As mathematical constructions go, you can’t get much more canonical than that! No fuss, no muss — it’s a purely categorical construction (categorists call it a counit of an adjunction). So then why didn’t I see that myself? 🙂

4. We’re still not sure what the story is in other dimensions. If $a_n$ is the maximum number of admissible colors in dimension $n$ , then about all any one of us knows right now is that $a_n = n$ for $n = 2^k$ , $a_n$ is weakly monotone increasing, and that $a_n < n$ if $n$ is not a power of 2. There’s a conjecture afloat that $a_n = 2^{\left[\log_2 n\right]}$ where $\left[x\right]$ is the floor function, but for now that should be treated as a wild guess. If anyone has further information, please let us know!

Solved by Arin Chaudhuri, David Eppstein, Sune Jakobsen, and Philipp Lampe. Thanks to all those who wrote in!

POW-12: A graph-coloring problem

December 26, 2008 in Elementary Math Problem Solving, Problem of the Week (POW) | Tags: graph coloring problems | by Todd Trimble | 4 comments

Happy holidays, folks! And happy birthday to Topological Musings, which Vishal started just a little over a year ago — we’ve both had a really good time with it.

And in particular with the Problem of the Week series. Which, as we all know, doesn’t come out every week — but then again, to pinch a line from John Baez’s This Week’s Finds, we never said it would: only that each time a new problem comes out, it’s always the problem for that week! Anyway, we’ve been very gratified by the response and by the ingenious solutions we routinely receive — please keep ’em coming.

This problem comes courtesy of regular problem-solver Arin Chaudhuri and — I’ll freely admit — this one defeated me. I didn’t feel a bit bad though when Arin revealed his very elegant solution, and I’d like to see what our readers come up with. Here it is:

What is the maximum number of colors you could use to color the vertices of an 8-dimensional cube, so that starting from any vertex, each color occurs as the color of some neighbor of that vertex? (Call two vertices neighbors if they are the two endpoints of an edge of the cube.)

Arin, Vishal, and I would be interested and pleased if someone solved this problem for all dimensions $n$ .

Please submit solutions to topological[dot]musings[At]gmail[dot]com by Friday, January 2, 2009, 11:59 pm (UTC); do not submit solutions in Comments. Everyone with a correct solution will be inducted into our Hall of Fame! We look forward to your response.

Solution to POW-11: Preserving sums of squares

November 4, 2008 in Elementary Math Problem Solving, Problem of the Week (POW) | by Todd Trimble | 9 comments

The solutions to POW-11 are in! Or make that solution, unless you also count your hosts’: only one reader responded. Perhaps everyone has been distracted by the upcoming US presidential election?!

Composite solution by Philipp Lampe, University of Bonn, and Todd and Vishal: We claim there are exactly two functions $h: \mathbb{N} \to \mathbb{N}$ which satisfy the identity $h(p^2 + q^2) = h(p)^2 + h(q)^2$ : the identity function and the function which is identically zero.

Clearly $h(0) = h(0^2 + 0^2) = 2h(0)^2$ forces $h(0) = 0$ , whence $h(1) = h(1^2 + 0^2) = h(1)^2$ . Therefore $h(1) = 0$ or $h(1) = 1$ , and the claim above follows if we show that $h(p) = ph(1)$ for all $p \in \mathbb{N}$ . The first few cases are built up as follows:

$h(2) = h(1^2 + 1^2) = 2h(1)^2 = 2h(1)$

$h(4) = h(2^2) = (2h(1))^2 = 4h(1)$

$h(5) = h(2^2 + 1^2) = (2h(1))^2 + h(1)^2 = 5h(1)$

$h(3) = \sqrt{h(3^2 + 4^2) - h(4)^2} = \sqrt{h(5)^2 - h(4)^2} = \sqrt{(25-16)h(1)^2}$

$= 3h(1)$

$h(8) = h(2^2 + 2^2) = (2h(1))^2 + (2h(1))^2 = 8h(1)$

$h(10) = h(3^2 + 1^2) = (3h(1))^2 + h(1)^2 = 10h(1)$

$h(6) = \sqrt{h(6^2 + 8^2) - h(8)^2} = \sqrt{h(10)^2 - h(8)^2}$

$= \sqrt{(100-64)h(1)^2} = 6h(1)$

where in a few places we have invoked the simple lemma that $h(p^2) = h(p)^2$ [since $h(p^2 + 0^2) = h(p)^2 + 0^2$ ]. The remainder of the argument proceeds by strong induction. For odd $p = 2m+1 > 5$ , we have

$(2m+1)^2 + (m-2)^2 = (2m-1)^2 + (m+2)^2 \qquad (1)$

Since $h$ preserves sums of two squares, we derive

$h(2m+1)^2 + h(m-2)^2 = h(2m-1)^2 + h(m+2)^2$

Therefore, using the inductive hypothesis that $h(q) = qh(1)$ for $q < 2m+1$ , we have

$h(2m+1)^2 + (m-2)^2h(1) = (2m-1)^2 h(1) + (m+2)^2 h(1) \qquad (2)$

From equation (1) we also have

$(2m+1)^2h(1) + (m-2)^2h(1) = (2m-1)^2h(1) + (m+2)^2h(1) \qquad (3)$

Comparing equations (2) and (3), we infer $h(2m+1) = (2m+1)h(1)$ . In particular, $h(q) = qh(1)$ for $q = 7, 9$ , and we have the case $h(8) = 8h(1)$ from before. This will be used to start the induction for even $p$ , starting from $p = 10$ .

For even $p = 2m+2$ , where $m \geq 4$ , we have

$(2m + 2)^2 + (m-4)^2 = (2m-2)^2 + (m+4)^2 \qquad (4)$

and by arguing as we did above, we derive the two equations

$h(2m+2)^2 + h(m-4)^2 = h(2m-2)^2 + h(m+4)^2$

$h(2m+2)^2 + (m-4)^2h(1) = (2m-2)^2h(1) + (m+4)^2h(1)$

where the second follows from the first by inductive hypothesis. Multiplying (4) through by $h(1)$ and comparing with the last equation, we conclude $h(2m+2) = (2m+2)h(1)$ , and this completes the proof.

Remarks:

The underlying idea is to exploit the fact that many numbers can be expressed as a sum of two squares in more than one way, so that one can generate enough relations of the form $h(p)^2 + h(q)^2 = h(r)^2 + h(s)^2$ to nail down all the $h(p)$ [in terms of $h(1)$ ]. A powerful way of generating equations of the form $p^2 + q^2 = r^2 + s^2$ is to consider prime factorizations in the ring of Gaussian integers $\mathbb{Z}\left[i\right]$ . For example, in the Gaussian integers we have the prime factorizations

$5 = (2 + i)(2-i) \qquad 13 = (2 + 3i)(2-3i)$

so that there are two ways of writing their product 65 in the form $z \cdot \bar{z}$ :

$(2+i)(2+3i) \cdot (2-i)(2-3i), \qquad (2+i)(2-3i) \cdot (2-i)(2+3i)$

Here we have, respectively, $z = 1 + 8i$ , $z = 7 - 4i$ , whence $65 = z \cdot \bar{z} = 1^2 + 8^2 = 7^2 + 4^2$ . Extrapolating from this, if we set

$z = (a+bi)(c+di), \qquad z' = (a+bi)(c-di)$

then we have $|z|^2 = z \cdot \bar{z} = z' \cdot \bar{z'} = |z'|^2$ , whence we derive

$(ac - bd)^2 + (bc + ad)^2 = (ac + bd)^2 + (bc - ad)^2.$

This gives a large supply of available relations to work with, and from there it is not too bad to get an inductive argument up and flying, once some base cases have been cleared out of the way with some numerical experimentation.

[Although it’s a little unusual to need such an outlay of base cases (up to at least $p = 6$ ) before one can start the induction; it creates a psychological hurdle, I feel. It reminds me of POW-6, where no complete solutions were received: one has to fiddle with a number of base cases before the general argument can be pushed through.]

Incidentally, while researching this problem, I found the wonderful website MathPages, created by an all but anonymous author named Kevin Brown. I really recommend checking out this website, and I hope that it is somehow kept alive: it would be a shame for such a treasure trove to be buried and forgotten in some deep hollow of cyberspace.

POW-11: Preserving sums of squares

October 26, 2008 in Elementary Math Problem Solving, Problem of the Week (POW) | by Todd Trimble | 4 comments

Time for another problem of the week! This one doesn’t necessarily require any number-theoretic knowledge, although a little bit might help point you in the right direction. As usual, let $\mathbb{N}$ be the set of natural numbers, i.e., the set of nonnegative integers.

Describe all functions $h: \mathbb{N} \to \mathbb{N}$ such that $h(p^2 + q^2) = h(p)^2 + h(q)^2$ for all $p, q \in \mathbb{N}$ .

Please submit solutions to topological[dot]musings[At]gmail[dot]com by Sunday, November 2, 11:59 pm (UTC); do not submit solutions in Comments. Everyone with a correct solution will be inducted into our Hall of Fame! We look forward to your response.

Solution to POW-10: Another hard integral?

October 12, 2008 in Elementary Math Problem Solving, Problem of the Week (POW) | Tags: integration | by Todd Trimble | 17 comments

The solutions are in! As is so often the case, solvers came up with a number of different approaches; the one which follows broadly represents the type of solution that came up most often. I’ll mention some others in the remarks below, some of it connected with the lore of Richard Feynman.

Solution by Nilay Vaish: The answer to POW-10 is $\displaystyle \frac{\pi}{2}\ln 2$ . Put

$\displaystyle I = \int_{0}^{\pi/2} \frac{x}{\tan x} dx = \int_{0}^{\pi/2} \frac{x\cos x}{\sin x} dx$

and integrate by parts: we have

$\displaystyle I = x\ln \sin x |_{0}^{\pi/2} - \int_{0}^{\pi/2} \ln \sin x dx.$

The first term vanishes by a simple application of L’hôpital’s rule. We now have

$\displaystyle I \stackrel{(1)}{=} -\int_{0}^{\pi/2} \ln \sin x dx = -\int_{0}^{\pi/2} \ln \cos x dx$

where the second equation follows from $\cos x = \sin(\pi/2 - x)$ , and the general elementary fact that $\int_{b}^{c} f(x) dx = \int_{a-c}^{a-b} f(a-x) dx.$ Adding the last two displayed equations, we obtain

$\displaystyle 2I = -\int_{0}^{\pi/2} \ln (\sin (x) \cos (x)) dx = -\int_{0}^{\pi/2} \ln(\frac{\sin 2x}{2}) dx.$

This gives

$\displaystyle 2I = \int_{0}^{\pi/2} \ln 2 dx - \int_{0}^{\pi/2} \ln \sin 2x dx = \frac{\pi \ln 2}{2} - \frac1{2} \int_{0}^{\pi} \ln \sin t dt \qquad (2)$

after a simple substitution. The last integral splits up as two integrals:

$\displaystyle \int_{0}^{\pi} \ln \sin t dt = \int_{0}^{\pi/2} \ln \sin t dt + \int_{\pi/2}^{\pi} \ln \sin t dt \qquad (3)$

but these two integrals are equal, using the identity $\sin t = \sin(\pi - t)$ together with the general integration fact cited above. Hence the two sides of (3) equal

$\displaystyle 2\int_{0}^{\pi/2} \ln \sin t dt = -2I \qquad (4),$

recalling equation (1) above. Substituting this for the last integral in equation (2), we arrive at

$\displaystyle 2I = \frac{\pi}{2} \ln 2 + I$

whence we derive the value of the desired integral $I$ .

Remarks:

1. A number of solvers exploited variations on the theme of the solution above, which could be summarized as involving symmetry considerations together with a double angle formula. For example, Philipp Lampe and Paul Shearer in their solutions made essential use of the identity

$2 \cot(2x) = \cot x - \tan x$

in conjunction with the complementarity $\cot x = \tan(\pi/2 - x)$ , and the general integration fact cited above.

2. Arin Chaudhuri (and Vishal in private email) pointed out to me that the evaluation of the integral

$\displaystyle \int_{0}^{\pi/2} \ln \sin x dx$

is actually fairly well-known: it appears for example in Complex Analysis by Ahlfors (3rd edition, p. 160) to illustrate contour integration of a complex analytic function via the calculus of residues, and no doubt occurs in any number of other places.

3. Indeed, Simon Tyler in his solution referred to this as an integral of Clausen type, and gave a clever method for evaluating it: we have

$\displaystyle \int_{0}^{\pi/2} \ln \sin x dx = \frac1{2}\int_{0}^{\pi/2} \ln \frac1{2} (1 - \cos 2x) dx$

which works out to

$\displaystyle -\frac{\pi \ln 2}{4} + \frac1{4}\int_{0}^{\pi} \ln(1 - \cos x) dx \qquad (*)$

The last integral can be expanded as a series

$\displaystyle -\sum_{n \geq 1} \int_{0}^{\pi} \frac1{n} \cos^n(x) dx$

where the summands for odd $n$ vanish; the other terms can be collected and then resummed to yield

$\displaystyle \frac1{2} \int_{0}^{\pi} \ln(1 - \cos^2 x) dx = \int_{0}^{\pi} \ln \sin x dx = 2 \int_{0}^{\pi/2} \ln \sin x dx$

and by substituting this for the integral in (*), the original integral is easily evaluated.

4. Arin C. later described still another method which he says he got from an exercise in a book by Apostol — it’s close in spirit to the one I myself had in mind, called “differentiation under the integral sign”, famously referred to in Surely You’re Joking, Mr. Feynman!. As Feynman recounts, he never really learned fancy methods like complex contour integration, but he did pick up this method of differentiating under the integral sign from an old calculus book. In typical Feynman style, he writes,

“It turns out that’s not taught very much in the universities; they don’t emphasize it. But I caught on how to use that method, and I used that one damn tool again and again. So because I was self-taught using that book [Wilson’s Advanced Calculus], I had peculiar methods of doing integrals. The result was, when guys at MIT or Princeton had trouble doing a certain integral, it was because they couldn’t do it with the standard methods they had learned in school. If it was contour integration, they would have found it; if it was a simple series expansion, they would have found it. Then I come along and try differentiating under the integral sign, and often it worked. So I got a great reputation for doing integrals, only because my box of tools was different from everybody else’s, and they had tried all their tools on it before giving the problem to me.”

So, what is this method? Wikipedia has a pretty good article on it; the idea is to view a given definite integral $\int_{a}^{b} f(x) dx$ as an instance of a smoothly parametrized family $G(t) = \int_{a}^{b} F(x, t) dx$ of integrals, where the extra parameter $t$ is inserted at some judicious spot, in such a way that $G(t)$ has an easy-to-integrate derivative. Then one figures out $G$ , and evaluates it at the $t$ which yields the original definite integral.

The best way to understand it is through an example. Pretend you’re Feynman, and someone hands you

$\displaystyle \int_{0}^{1} \frac{x^{10} - 1}{\ln x} dx$

[I suppose there may be a contour integration method to handle that one, but never mind — you’re Feynman now, and not supposed to know how to do that!] After fiddling around a little, you find that by inserting a parameter $t$ in the exponent,

$\displaystyle G(t) := \int_{0}^1 \frac{x^{10 t} - 1}{\ln x} dx,$

this $G(t)$ has a very simple derivative:

$\displaystyle G'(t) = \frac{d}{dt} \int_{0}^{1} \frac{x^{10 t} - 1}{\ln x} dx = \int_{0}^{1} \frac{\partial}{\partial t} \frac{x^{10 t} - 1}{\ln x} dx$

i.e., by differentiating under the integral sign, you manage to kill off that annoying factor $\ln x$ in the denominator:

$\displaystyle G'(t) = \int_{0}^{1} 10 x^{10 t} dx = \frac{10 x^{10 t + 1}}{10 t + 1} |_{0}^{1} = \frac{10}{10 t + 1}.$

We therefore have

$G(t) = \ln(10 t + 1) + C,$

and notice that from the original definition of $G(t)$ , we have $G(0) = 0$ . Thus $C = 0$ , and the problem integral evaluates to $G(1) = \ln 11$ . Bam!

It takes a little experience to judge where or how to stick in the extra parameter $t$ to make this method work, but the Wikipedia article has some good practice problems, including the integral of POW-10. For this problem they recommend considering

$\displaystyle G(t) = \int_{0}^{\pi/2} \frac{\tan^{-1} (t\tan x)}{\tan x} dx$

and I’ll let you the reader take it from there.

The point is not that this method is much more elegant than others, but that a little practice with it should be enough to convince one that it’s incredibly powerful, and often succeeds where other methods fail. (Not always, of course, and Feynman had to concede defeat when in response to a challenge, his pal Paul Olum concocted some hellacious integral which he said could only be done via contour integration.)

Doron Zeilberger is also fond of this method (as witnessed by this paper). Something about it makes me wonder whether it’s secretly connected with the idea of “creative telescoping” and the powerful methods (e.g., see here) developed by Gosper, Wilf, Zeilberger, and others to establish identities of hypergeometric type. But I haven’t had time to consider this carefully.

Also solved by Arin Chaudhuri, Philipp Lampe (University of Bonn), Paul Shearer (University of Michigan), and Simon Tyler. Thanks to all who wrote in!

POW-10: Another hard integral?

October 4, 2008 in Elementary Math Problem Solving, Problem of the Week (POW) | by Todd Trimble | 4 comments

Another problem of the week has been long overdue. Here’s one that may appeal to those who liked POW-5 (maybe we should have an integration problem every fifth time?):

Evaluate $\displaystyle \int_{0}^{\pi/2} \frac{x}{\tan x} dx.$

Please submit solutions to topological[dot]musings[At]gmail[dot]com by Friday, October 10, 11:59 pm (UTC); do not submit solutions in Comments. Everyone with a correct solution will be inducted into our Hall of Fame! We look forward to your response.

Almost a problem of the week

September 28, 2008 in Elementary Math Problem Solving, Problem of the Week (POW) | Tags: continued fractions, generating functions, pell's equation | by Todd Trimble | 4 comments

It’s been quite a while since I’ve posted anything; I’ve been very busy with non-mathematical things this past month, and probably will be for at least another few weeks. In the meantime, I’d been idly thinking of another Problem of the Week to post, and while I was thinking of one such problem… I got stuck. So instead of just baldly posing the problem, this time I’ll explain how far as I got with it, and then ask you all for help.

The problem is easy to state: except for 1, are there any positive integers which are simultaneously triangular, square, and pentagonal numbers?

Just asking for all numbers which are simultaneously triangular and square is a fun little exercise in number theory, involving Pell’s equation and (yes) continued fractions. I’ll sketch how this goes. We are trying to solve the Diophantine equation

$\displaystyle m^2 = \frac{n(n+1)}{2}$

By completing the square and manipulating a little, we get

$8m^2 = (2n+1)^2 - 1.$

This converts to a Pell equation $x^2 - 2y^2 = 1$ where $x = 2n+1$ , $y = 2m$ . Writing the Pell equation as

$N(x + \sqrt{2}y) := (x + \sqrt{2}y)(x - \sqrt{2}y) = 1,$

and using the fact that the norm map $N: \mathbb{Q}(\sqrt{2}) \to \mathbb{Q}$ just defined is a multiplicative homomorphism (because the Galois automorphism $x + \sqrt{2}y \mapsto x - \sqrt{2}y$ is also multiplicative), we see that the set of solutions

$\{(x, y): N(x + \sqrt{2}y) = 1\}$

forms a group, under the group multiplication law

$(x, y) \cdot (x', y') = (x x' + 2y y', x y' + y x')$

which is read off just by expanding $(x + \sqrt{2}y)(x' + \sqrt{2}y')$ . The right branch of the hyperbola $x^2 - 2y^2 = 1$ thus forms a group (under this multiplication law, with identity $(1, 0)$ ) which is isomorphic to the additive group of real numbers. The set of integer solutions sitting on this branch forms a discrete subgroup, and hence is isomorphic to the additive group of integers (provided that nontrivial solutions exist!). To find a generator of this group, just look for the integer solutions to $x^2 - 2y^2 = 1$ which come closest to the identity $(1, 0)$ ; they are $(x, y) = (3, 2), (3, -2)$ .

So, $(3, 2)$ generates the set of positive integer solutions. The next is

$(3, 2)^2 = (3 \cdot 3 + 2(2 \cdot 2), 3 \cdot 2 + 2 \cdot 3) = (17, 12)$

and in general, the solutions $(x_n, y_n) = (3, 2)^n$ are given recursively by

$(x_n, y_n) = (3x_{n-1} + 4y_{n-1}, 2x_{n-1} + 3y_{n-1}).$

Let’s go back a minute to our original problem, which asked for numbers which are both triangular and square. We read off the $k^{th}$ triangle-square, $m_k^2 = n_k(n_k+1)/2$ , from $(x_k, y_k) = (2n_k + 1, 2m_k)$ . For example,

$(x_2, y_2) = (17, 12) \Rightarrow (n_2, m_2) = (8, 6)$

and so the square $36 = 6^2$ is simultaneously the triangular number $1 + 2 + \ldots + 8$ . From $(x_3, y_3) = (99, 70)$ , we have $(m_3, n_3) = (49, 35)$ , and so $35^2$ is the next triangle-square. The next after that is $204^2$ . And so on.

It would be nice to express these solutions in closed form. To this end, let me observe that the quotients $x_k/y_k = 3/2, 17/12, 99/70, \ldots$ are rational approximants to the continued fraction of $\sqrt{2}$ :

$3/2 = 1 + 1/2,$

$17/12 = 1 + 1/(2 + 1/(2 + 1/2)),$

$99/70 = 1 + 1/(2 + 1/(2 + 1/2 + 1/(2 + 1/2), \ldots$

(A similar observation applies to any Pell equation: positive solutions to $x^2 - Dy^2 = 1$ , where $D$ is square-free, can be read off by examining every other rational approximant to the continued fraction for $\sqrt{D}$ . This, I find, is a very cool fact.)

Starting from the first two rational approximants $p_0/q_0 = 1/1, p_1/q_1 = 3/2$ , the remaining approximants $p_k/q_k$ can be read off from the recursive rule (*)

$p_{k+1} = 2p_k + p_{k-1} \qquad q_{k+1} = 2q_k + q_{k-1}$

and for the purpose of determining the triangle-squares, we are really interested only in every other one of the denominators $q_k$ , that is to say, $q_1, q_3, q_5, \ldots$ . We can get a recursive rule for these from

$q_{k+2} = 2q_{k+1} + q_k = 2(2q_k + q_{k-1}) + q_k = 6q_k - q_{k-2}$

where the last equation follows easily from the recursive rule (*). The same recursion thus gives the $y_k$ and $m_k$ :

$y_k = 2, 12, 70, 408, \ldots,$

$m_k = 1, 6, 35, 204, \ldots,$

namely $m_k = 6m_{k-1} - m_{k-2}$ .

To get a closed form for the $m_k$ (whose squares are triangular), we can now apply the familiar method of generating functions (see here for a worked example of this method to derive the closed form for the Fibonacci numbers). Form

$f(x) = m_1 + m_2 x + m_3 x^2 + \ldots = 1 + 6x + 35x^2 + \ldots$

and use the recursive rule for the $m_k$ to deduce (after some manipulation) that

$\displaystyle f(x) = \frac1{1 - 6x + x^2}.$

The denominator expands as $(1 - (3 + \sqrt{8})x)(1 - (3 - \sqrt{8})x)$ ; by the method of partial fractions, we obtain

$\displaystyle f(x) = \frac{(3 + \sqrt{8})/2\sqrt{8}}{1 - (3 + \sqrt{8})x} - \frac{(3 - \sqrt{8})/2\sqrt{8}}{1 - (3 - \sqrt{8})x}$

and from there, expanding the preceding line in geometric series, we derive a closed form for the $m_k$ :

$\displaystyle m_k = \frac1{2\sqrt{8}}((3 + \sqrt{8})^k - (3 - \sqrt{8})^k)$

Nice! If you prefer, this is just the integer part of $\displaystyle \frac1{2\sqrt{8}}(3 + \sqrt{8})^k$ .

So, the $k^{th}$ triangular square is

$\displaystyle \frac1{32}((3 + \sqrt{8})^{2k} + (3 - \sqrt{8})^{2k} - 2).$

Sweet.

Having gone through this analysis, the same method can be used to determine those squares which are pentagonal (the first few pentagonal numbers are $1, 1+4, 1+4+7, 1+4+7+10, \ldots$ ). I’ll let readers work this out if they like; suffice it to say that the $k^{th}$ square which is also pentagonal is the square of

$\displaystyle \frac1{2\sqrt{24}}((5 + \sqrt{24})^{2k-1} - (5 - \sqrt{24})^{2k-1}).$

And that’s about as far as I got with this. After trying a few numerical forays with a hand-held calculator, my gut feeling is that I’d be amazed if there were any triangular-square-pentagonals past $m = 1$ . But can anyone clinch the case?

[Edit: I’ve corrected the exponents in the last displayed line, from $k$ to $2k-1$ .]

Solution to POW-9: Period of a decimal expansion

August 30, 2008 in Elementary Math Problem Solving, Problem of the Week (POW) | Tags: quadratic reciprocity | by Todd Trimble | 5 comments

The solutions are in! Last week’s POW-9 is a problem for which you need a bit of insight to solve at all (even with calculator or computer), and then a bit more to solve elegantly without machine aid.

Solution by Philipp Lampe, University of Bonn: The answer is $n = 65536$ . The decimal expansion of 1/65537 is eventually periodic with (minimum) period length $n$ . Suppose it takes the form

$\displaystyle s \cdot 10^{-k} + t \cdot 10^{-(k+n)} + t \cdot 10^{-(k + 2n)} + t \cdot 10^{-(k + 3n)} + \ldots$

$\displaystyle = \frac{s}{10^k} + \frac{t}{10^k (10^n - 1)}$

for integers $0 \leq s < 10^k$ and $0 \leq t < 10^n$ . Then $65537| 10^k (10^n - 1)$ , and therefore $65537|10^n - 1$ ; equivalently $10^n \equiv 1 \mod 65537$ . The minimum $m$ such that $10^m \equiv 1 \mod 65537$ (i.e., the order of 10 modulo 65537) must then divide $n$ . On the other hand, from $65537u = 10^m - 1$ , we derive

$\displaystyle \frac1{65537} = \frac{u}{10^m - 1} = \frac{u}{10^m} + \frac{u}{10^{2m}} + \ldots$

Thus by minimality of $n$ , we conclude $m = n$ , and that the decimal expansion is periodic (not merely eventually periodic).

It is well known that $p = 65537 = 2^{16} + 1$ is prime (it is the largest known Fermat prime), so by Fermat’s little theorem, the order of 10 modulo $p$ divides $\phi(p) = p - 1 = 2^{16}$ (where $\phi$ is the Euler phi-function), and so it must be a power of 2, at most $2^{16}$ . That the order is in fact $2^{16}$ can be checked either by brute force (by repeated squaring and reduction modulo 65537, best carried out with calculator or computer), or by the following number-theoretic argument.

Since $p$ is prime, the multiplicative group of nonzero elements of the field $\mathbb{Z}_p$ is cyclic (is generated by a single element, say $a$ ). Hence $10 \equiv a^i \mod p$ where $1 \leq i < 65536$ , and $10$ itself is a generator (has order 65536) iff $i$ is prime to 65536, i.e., iff $i$ is odd. This occurs iff 10 is a non-square modulo $p$ . Defining the Jacobi symbol by the usual formula

$\displaystyle (\frac{a^i}{p}) = (-1)^i$

(so that $(\frac{x}{p}) = 1$ iff $x$ is a square modulo $p$ ), we have

$\displaystyle (\frac{10}{p}) = (\frac{2}{p}) \cdot (\frac{5}{p})$

The second factor is, by the law of quadratic reciprocity (and the fact $p \equiv 1 \pmod 4$ ),

$\displaystyle (\frac{5}{p}) = (\frac{p}{5}) = (\frac{2}{5}) = -1.$

Also, by the “second supplement“, we compute $(\frac{2}{p}) = (-1)^{(p^2 - 1)/8} = 1$ . Hence $(\frac{10}{p}) = -1$ : 10 is a non-square as desired. This completes the proof.

Remarks:The argument in the first paragraph of Philipp’s solution proves for 1/65537 a fact which holds generally for any reduced fraction $0 < q/p < 1$ where $p$ is prime to 10: that the decimal expansion is actually periodic, not just eventually periodic. Henry Wilton also took the time and trouble to argue this point. I’m not sure how widely known that is, so I was glad the point was made; of course the main thing we need from that paragraph is the general fact that the period length of $q/p$ equals the order of 10 modulo $p$ .

A number of solvers computed the order of 10 by brute force, which I accepted. The use of quadratic reciprocity is slick but gets into rather deeper waters. As the Wikipedia article explains, this law was known to (or at least conjectured by) Euler and Legendre, but resisted a complete proof until Gauss found one after an intensive effort; it was one of his proudest achievements, and a theorem he returned to over the decades, giving over half a dozen more proofs in his life. Now more than 200 proofs are known. One proof that I like was given by Zolotarev, which is given a nice account in an appendix to John Conway’s very entertaining book, The (Sensual) Quadratic Form. Arin Chaudhuri pointed out to me that it’s also given as an exercise in Knuth’s The Art of Computer Programming (Vol. I, p. 45, exercise 47).

The “second supplement” was, according to the Wikipedia article, first proved by Euler. Its use here can be circumvented by observing that 2 cannot have order $p -1 = 65536$ since already $2^{16} = -1 \mod p$ , so that by Lampe’s argument, 2 is a square mod $p$ , i.e. $(\frac{2}{p}) = 1$ .

Quadratic reciprocity is no isolated curiosity: most of the deeper, more conceptual treatments involve some nontrivial algebraic number theory, and the efforts to formulate reciprocity laws for higher powers had a lot to do with the creation of class field theory, culminating in Artin reciprocity, one of the crowning achievements of early 20th century mathematics.

Also solved by Arin Chaudhuri, Ashwin Kumar, Vladimir Nesov, Américo Tavares, Nathan Williams, and Henry Wilton. Thanks to all who wrote in!

	Strong equidistribut… on Platonic Solids and Euler…
	m.s.mohamed ansari on The 54th Carnival of Math…
	Convictions ·… on Continued fraction for e
	Wayne J. Mann on Solution to POW-12: A graph co…
	erneststephen on The 54th Carnival of Math…
	anhtraisg on p^q + q^p is prime
	prof dr drd horia or… on My first post
	prof drd horia orasa… on My first post
	prof dr mircea orasa… on Inequality with log
	notedscholar on Self-referential Paradoxes, In…
	prof dr mircea orasa… on Inequality with log
	prof dr mircea orasa… on Inequality with log
	prof dr mircea orasa… on 2010 in review
	kenji on Basic category theory, I
	prof dr mircea orasa… on Solution to POW-10: Another ha…

Category Archive

Solution to POW-13: Highly coincidental!

POW-13: Highly coincidental!

Solution to POW-12: A graph coloring problem

POW-12: A graph-coloring problem

Solution to POW-11: Preserving sums of squares

POW-11: Preserving sums of squares

Solution to POW-10: Another hard integral?

POW-10: Another hard integral?

Almost a problem of the week

Solution to POW-9: Period of a decimal expansion

Our other blog

Visitors to this blog

Blog Stats

Wikio Ranking

Current Online Readers

Recent Comments

Top Posts

Archives

Categories

Blogroll

chess

Computers and Technology

Elementary Math Problem Solving

Fun, Humor

Higher Mathematics

Math Education

Non-technical

Opinions

People in Computer Science

People in mathematics

Philosophy & Logic

Physics

Politics, News

Sciences

Useful general links

Useful Math Links

Tag Cloud

Admin/Users Login

Pages