The following theorem, I feel, is not very well-known, though it is a particularly useful one for solving certain types of “limit” problems. Let me pose a couple of elementary problems and offer their solutions. First, the theorem.
Stolz-Cesàro: Let and
be two sequences of real numbers, such that
is positive, strictly increasing and unbounded. Then,
,
if the limit on the right hand side exists.
The proof involves the usual method, and I will avoid presenting it here since it isn’t particularly interesting. Just as Abel’s lemma is the discrete analogue of integration by parts, the Stolz-Cesàro theorem may be considered the discrete analogue of L’Hospital’s rule in calculus.
Problem 1: Evaluate the limit , where
.
Solution: One may certainly consider the above limit as a Riemann-sum which may then be transformed into the integral , which then obviously evaluates to
. But, we will take a different route here.
First, let and
. Then, we note that the sequence
is positive, strictly increasing and unbounded. Now,
(using the binomial theorem)
.
Therefore, using the Stolz-Cesàro theorem, we conclude that the required limit is also .
Let us now look at another problem where applying the aforesaid theorem makes our job a lot easier. This problem is an example of one that is not amenable to the other usual methods of evaluating limits.
Problem 2: Let be integers and suppose
. Given the tangent line at the point
from the point
to
, evaluate
.
Solution:(This is basically the solution I had offered elsewhere a while ago; so, it’s pretty much copy/paste!)
.
So, the equation of the tangent line at the point is given by
Since the point lies on this line, we must have
The above, after squaring and some algebraic manipulation yields
, which implies
. We drop the negative root because
for all
.
(This is where the Stolz-Cesàro theorem actually comes into play!)
Now, let and
be two sequences such that
and
Note that is a positive, increasing and unbounded sequence.
Therefore,
.
Therefore, by the Stolz- Cesàro theorem, we have
, and so
.

19 comments
Comments feed for this article
May 8, 2008 at 5:15 pm
John Armstrong
cite
September 19, 2012 at 10:41 am
Luqing Ye
Abel’s lemma can be used to prove integration by parts.Stolz’s theorem can be used to prove L’Hospital’s law.
May 8, 2008 at 11:40 pm
Todd Trimble
Re the proof of Stolz-Cesàro: there’s the fun little fact that if and
and  , then
, then
(“the quotient sum of two fractions is between the two fractions”). It follows that if the fractions are in the interval
are in the interval 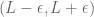 for
for 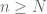 , then so are all the “telescoping quotient sums”
, then so are all the “telescoping quotient sums”  . Since the
. Since the  grow without bound,
grow without bound,  is also in this interval for
is also in this interval for  sufficiently large. The conclusion follows.
sufficiently large. The conclusion follows.
May 9, 2008 at 1:47 am
Vishal Lama
Todd,
That is a wonderful proof! Thanks for sharing it. I hope you won’t mind if I incorporate the proof in the post some time later. I may perhaps expand a few steps just so that some of our readers may find it easier to see what you just did.
May 9, 2008 at 7:40 pm
John Armstrong
Another consequence of the lemma Todd states is that batting averages actually behave like averages, in that they lie in the middle of the data.
May 10, 2008 at 1:14 am
misha
There is still another neat way to figure out the limit in problem 1. It is based on the combinatorial identity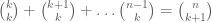 that says that to pick k+1 numbers from 1,2,3,…,n you need first to pick your biggest number and then the rest k of them.
that says that to pick k+1 numbers from 1,2,3,…,n you need first to pick your biggest number and then the rest k of them.
May 10, 2008 at 1:43 am
misha
Still another proof of Stolz-Cesàro. Extend the sequences to piecewise-linear functions by linearly interpolatiing between n and n+1. Then you can either notice that L’Hospital’s rule holds for comtinuous piecewise-differentiable functions, or smooth out the corners and use L’Hospital directly.
May 10, 2008 at 5:02 am
Vishal Lama
Misha,
Those are awesome proofs! Thanks very much!
May 10, 2008 at 7:03 am
misha
Still another way to look at Stolz-Cesàro, that makes it sort of obvious. Begin by linear interpolation, like in my previous comment, then take b as the independent variable.
May 11, 2008 at 6:47 am
misha
That made me think about the alternative proof of the L’Hospitals’s rule itself. Just take the denominator as the independent variable etc.
May 16, 2008 at 4:35 am
Ars Mathematica » Blog Archive » Stolz-Cesaro Theorem
[…] Musings has a post up about a cute little result, the Stolz-Cesaro theorem. The result is a discrete analogue of l’Hôpital’s […]
December 19, 2017 at 11:24 am
merniu
here is indeed as say prof dr mircea orasanu and prof horia orasanu
November 21, 2018 at 9:03 am
dunsu
as indeed observed prof dr mircea orasanu
November 21, 2018 at 9:14 am
cionogiu
here we observed many aspects how as prof dr mircea orasanu and prof drd horia orasanu as followed and the famous orasanu m theorems of Laguerre but appear and calugaritza , arghiriade that have some little exercises or n dinculeanu with some insignificance propositions
November 21, 2018 at 9:21 am
casadudu
thus that Stolz – Cesato theorem is very fundamental in more parts of mathematical analyses and same Kummer Criterion for many ex4ercises ,therefore must study a great book of exercises for sequences or series due to prof dr mircea orasanu as 200 pages , ,and also most beauty theorem with consequences
December 1, 2018 at 11:38 pm
ceanegiu
in more and situations Stolz – Cesaro theorem can be extended as in case of series observed prof dr mircea orasanu and prof drd horia orasanu
December 6, 2018 at 12:23 pm
cimagiu
the importance of Stolz Cesaro theorem observed prof dr mircea orasanu is obviously that what j.r ockendon daniela nedelcu and other have not known and can be extended for Kummer problem
January 16, 2019 at 12:06 pm
casaguhu
these indeed happened and prof dr Constantin Udriste applied a correction specially for Riemann theory and Adrien Legendre for crucial discovered concerning elliptic integrals or collaboration with Riemann , Hilbert or Lagrange ,that discovered LAGRANGIAN ,but this is impossible FAC MATHEM Buch
February 21, 2019 at 9:21 am
fanfsanu
that is with these appear important aspects and then for prof dr mircea orasanu and prof drd horia orasanu and for CONSTRAINTS OPTIMIZATIONS followed in case of Joseph Gergonne works where our contribution have significance in full sense ,and these have more insight in sense of geometrical theory where prof dr mircea orasanu and Gergonne have many contributions . Thus Gergonne enlisted in the French army as a captain. That army was undergoing rapid expansion because the French government feared a foreign invasion intended to undo the French Revolution and restore Louis XVI to the throne of France. He saw action in the major battle of Valmy on 20 September 1792. He then returned to civilian life but soon was called up again and took part in the French invasion of Spain in 1794. and these geometrical theory have extended the MONGE GEOMETRY and Bezout Theory. Also these concepts contributed at OPTIMIZATIONS considerations elaborate by prof dr Constantin Udriste and also Brianchon theory