Basic Category Theory, III: Representability, adjoints, and the Yoneda lemma

In our last post on category theory, we continued our exploration of universal properties, showing how they can be used to motivate the concept of natural transformation, the “right” notion of morphism between functors . In today’s post, I want to turn things around, applying the notion of natural transformation to explain generally what we mean by a universal construction. The key concept is the notion of representability, at the center of a circle of ideas which includes the Yoneda lemma, adjoint functors, monads, and other things — it won’t be possible to talk about all these things in detail (because I really want to return to Stone duality before long), but perhaps these notes will provide a key of entry into more thorough treatments.

Even for a fanatic like myself, it’s a little hard to see what would drive anyone to study category theory except a pretty serious “need to know” (there is a beauty and conceptual economy to categorical thinking, but I’m not sure that’s compelling enough motivation!). I myself began learning category theory on my own as an undergraduate; at the time I had only the vaguest glimmerings of a vast underlying unity to mathematics, but it was only after discovering the existence of category theory by accident (reading the introductory chapter of Spanier’s Algebraic Topology) that I began to suspect it held the answer to a lot of questions I had. So I got pretty fired-up about it then, and started to read Mac Lane’s Categories for the Working Mathematician. I think that even today this book remains the best serious introduction to the subject — for those who need to know! But category theory should be learned from many sources and in terms of its many applications. Happily, there are now quite a few resources on the Web and a number of blogs which discuss category theory (such as The Unapologetic Mathematician) at the entry level, with widely differing applications in mind. An embarrassment of riches!

Anyway, to return to today’s topic. Way back when, when we were first discussing posets, most of our examples of posets were of a “concrete” nature: sets of subsets of various types, ordered by inclusion. In fact, we went a little further and observed that any poset could be represented as a concrete poset, by means of a “Dedekind embedding” (bearing a familial resemblance to Cayley’s lemma, which says that any group can be represented concretely, as a group of permutations). Such concrete representation theorems are extremely important in mathematics; in fact, this whole series is a trope on the Stone representation theorem, that every Boolean algebra is an algebra of sets! With that, I want to discuss a representation theorem for categories, where every (small) category can be explicitly embedded in a concrete category of “structured sets” (properly interpreted). This is the famous Yoneda embedding.

This requires some preface. First, we need the following fundamental construction: for every category there is an opposite category , having the same classes of objects and morphisms as , but with domain and codomain switched (, and ). The function is the same in both cases, but we see that the class of composable pairs of morphisms is modified:

[is a composable pair in ] if and only if

and accordingly, we define composition of morphisms in in the order opposite to composition in :

in .

Observation: The categorical axioms are satisfied in the structure if and only if they are in ; also, .

This observation is the underpinning of a Principle of Duality in the theory of categories (extending the principle of duality in the theory of posets). As the construction of opposite categories suggests, the dual of a sentence expressed in the first-order language of category theory is obtained by reversing the directions of all arrows and the order of composition of morphisms, but otherwise keeping the logical structure the same. Let me give a quick example:

Definition: Let be objects in a category . A coproduct of and consists of an object and maps , (called injection or coprojection maps), satisfying the universal property that given an object and maps , , there exists a unique map such that and .

This notion is dual to the notion of product. (Often, one indicates the dual notion by appending the prefix “co” — except of course if the “co” prefix is already there; then one removes it.) In the category of sets, the coproduct of two sets may be taken to be their disjoint union , where the injections are the inclusion maps of into (exercise).

Exercise: Formulate the notion of coequalizer (by dualizing the notion of equalizer). Describe the coequalizer of two functions (in the category of sets) in terms of equivalence classes. Then formulate the notion dual to that of monomorphism (called an epimorphism), and by a process of dualization, show that in any category, coequalizers are epic.

Principle of duality: If a sentence expressed in the first-order theory of categories is provable in the theory, then so is the dual sentence. Proof (sketch): A proof of a sentence proceeds from the axioms of category theory by applying rules of inference. The dualization of proves the dual sentence by applying the same rules of inference but starting from the duals of the categorical axioms. A formal proof of the Observation above shows that collectively, the set of categorical axioms is self-dual, so we are done.

Next, we introduce the all-important hom-functors. We suppose that is a locally small category, meaning that the class of morphisms between any two given objects is small, i.e., is a set as opposed to a proper class. Even for large categories, this condition is just about always satisfied in mathematical practice (although there is the occasional baroque counterexample, like the category of quasitopological spaces).

Let denote the category of sets and functions. Then, there is a functor

which, at the level of objects, takes a pair of objects to the set of morphisms (in ) between them. It takes a morphism of (that is to say, a pair of morphisms of ) to the function

Using the associativity and identity axioms in , it is not hard to check that this indeed defines a functor . It generalizes the truth-valued pairing we defined earlier for posets.

Now assume is small. From last time, there is a bijection between functors

and by applying this bijection to , we get a functor

This is the famous Yoneda embedding of the category . It takes an object to the hom-functor . This hom-functor can be thought of as a structured, disciplined way of considering the totality of morphisms mapping into the object , and has much to do with the Yoneda Principle we stated informally last time (and which we state precisely below).

• Remark: We don’t need to be small to talk about ; local smallness will do. The only place we ask that be small is when we are considering the totality of all functors , as forming a category .

Definition: A functor is representable (with representing object ) if there is a natural isomorphism of functors.

The concept of representability is key to discussing what is meant by a universal construction in general. To clarify its role, let’s go back to one of our standard examples.

Let be objects in a category , and let be the functor ; that is, the functor which takes an object of to the set . Then a representing object for is a product in . Indeed, the isomorphism between sets simply recapitulates that we have a bijection

between morphisms into the product and pairs of morphisms. But wait, not just an isomorphism: we said a natural isomorphism (between functors in the argument ) — how does naturality figure in?

Enter stage left the celebrated

Yoneda Lemma: Given a functor and an object of , natural transformations are in (natural!) bijection with elements .

Proof: We apply the “Yoneda trick” introduced last time: probe the representing object with the identity morphism, and see where takes it: put . Incredibly, this single element determines the rest of the transformation : by chasing the element around the diagram

                phi_c
      hom(c, c) -----> Fc
          |            |
hom(f, c) |            | Ff
          V            V
      hom(b, c) -----> Fb
                phi_b

(which commutes by naturality of ), we see for any morphism in that . That the bijection

is natural in the arguments we leave as an exercise.

Returning to our example of the product as representing object, the Yoneda lemma implies that the natural bijection

is induced by the element , and this element is none other than the pair of projection maps

In summary, the Yoneda lemma guarantees that a hom-representation of a functor is, by the naturality assumption, induced in a uniform way from a single “universal” element . All universal constructions fall within this general pattern.

Example: Let be a category with products, and let be objects. Then a representing object for the functor is an exponential ; the universal element is the evaluation map .

Exercise: Let be a pair of parallel arrows in a category . Describe a functor which is represented by an equalizer of this pair (assuming one exists).

Exercise: Dualize the Yoneda lemma by considering hom-functors . Express the universal property of the coproduct in terms of representability by such hom-functors.

The Yoneda lemma has a useful corollary: for any (locally small) category , there is a natural isomorphism

between natural transformations between hom-functors and morphisms in . Using as alternate notation for the hom-set, the action of the Yoneda embedding functor on morphisms gives an isomorphism between hom-sets

the functor is said in that case to be fully faithful (faithful means this action on morphisms is injective for all , and full means the action is surjective for all ). The Yoneda embedding thus maps isomorphically onto the category of hom-functors valued in the category .

It is illuminating to work out the meaning of this last statement in special cases. When the category is a group (that is, a category with exactly one object in which every morphism is invertible), then functors are tantamount to sets equipped with a group homomorphism , i.e., a left action of , or a right action of . In particular, is the underlying set of , equipped with the canonical right action , where . Moreover, natural transformations between functors are tantamount to morphisms of right -sets. Now, the Yoneda embedding

identifies any abstract group with a concrete group , i.e., with a group of permutations — namely, exactly those permutations on which respect the right action of on itself. This is the sophisticated version of Cayley’s theorem in group theory. If on the other hand we take to be a poset, then the Yoneda embedding is tantamount to the Dedekind embedding we discussed in the first lecture.

Tying up a loose thread, let us now formulate the “Yoneda principle” precisely. Informally, it says that an object is determined up to isomorphism by the morphisms mapping into it. Using the hom-functor to collate the morphisms mapping into , the precise form of the Yoneda principle says that an isomorphism between representables corresponds to a unique isomorphism between objects. This follows easily from the Yoneda lemma.

But far and away, the most profound manifestation of representability is in the notion of an adjoint pair of functors. “Free constructions” give a particularly ubiquitous class of examples; the basic idea will be explained in terms of free groups, but the categorical formulation applies quite generally (e.g., to free monoids, free Boolean algebras, free rings = polynomial algebras, etc., etc.).

If is a set, the free group (q.v.) generated by is, informally, the group whose elements are finite “words” built from “literals” which are the elements of and their formal inverses, where we identify a word with any other gotten by introducing or deleting appearances of consecutive literals or . Janis Joplin said it best:

Freedom’s just another word for nothin’ left to lose…

— there are no relations between the generators of beyond the bare minimum required by the group axioms.

Categorically, the free group is defined by a universal property; loosely speaking, for any group , there is a natural bijection between group homomorphisms and functions

where denotes the underlying set of the group. That is, we are free to assign elements of to elements of any way we like: any function extends uniquely to a group homomorphism , sending a word in to the element in .

Using the usual Yoneda trick, or the dual of the Yoneda trick, this isomorphism is induced by a universal function , gotten by applying the bijection above to the identity map . Concretely, this function takes an element to the one-letter word in the underlying set of the free group. The universal property states that the bijection above is effected by composing with this universal map:

where the first arrow refers to the action of the underlying-set or forgetful functor , mapping the category of groups to the category of sets ( “forgets” the fact that homomorphisms preserve group structure, and just thinks of them as functions ).

• Remark: Some people might say this a little less formally: that the original function is retrieved from the extension homomorphism by composing with the canonical injection of the generators . The reason we don’t say this is that there’s a confusion of categories here: properly speaking, belongs to the category of groups, and to the category of sets. The underlying-set functor is a device we apply to eliminate the confusion.

In different words, the universal property of free groups says that the functor , i.e., the underlying functor followed by the hom-functor , is representable by the free group : there is a natural isomorphism of functors from groups to sets:

Now, the free group can be constructed for any set . Moreover, the construction is functorial: defines a functor . This is actually a good exercise in working with universal properties. In outline: given a function , the homomorphism is the one which corresponds bijectively to the function

i.e., is defined to be the unique map such that .

Proposition: is functorial (i.e., preserves morphism identities and morphism composition).

Proof: Suppose , is a composable pair of morphisms in . By universality, there is a unique map , namely , such that . But also has this property, since

(where we used functoriality of in the first equation). Hence . Another universality argument shows that preserves identities.

Observe that the functor is rigged so that for all morphisms ,

That is to say, that there is only one way of defining so that the universal map is (the component at of) a natural transformation !

The underlying-set and free functors , are called adjoints, generalizing the notion of adjoint in truth-valued matrix algebra: we have an isomorphism

natural in both arguments . We say that is left adjoint to , or dually, that is right adjoint to , and write . The transformation is called the unit of the adjunction.

Exercise: Define the construction dual to the unit, called the counit, as a transformation . Describe this concretely in the case of the free-underlying adjunction between sets and groups.

What makes the concept of adjoint functors so compelling is that it combines representability with duality: the manifest symmetry of an adjunction means that we can equally well think of as representing as we can as representing . Time is up for today, but we’ll be seeing more of adjunctions next time, when we resume our study of Stone duality.

[Tip of the hat to Robert Dawson for the Janis Joplin quip.]

36th Carnival of Mathematics

I wish to bring the attention of our readers to the Carnival of Mathematics hosted by Charles at Rigorous Trivialities. I guess most of you already know about it. Among other articles/posts, one of Todd’s recent post Basic Category Theory I is part of the carnival. He followed it up with another post titled Basic Category Theory II. There will be a third post on the same topic some time soon. This sub-series of posts on basic category theory, if you recall, is part of the larger series on Stone Duality, which all began with Toward Stone Duality: Posets and Meets. Hope you enjoy the Carnival!

Basic Category Theory, II

I’ll continue then with this brief subseries on category theory. Today I want to talk more about universal properties, and about the notion of natural transformation. Maybe not today, but soon at any rate, I want to tie all this in with the central concept of representability, which leads directly and naturally to the powerful and fundamental idea of adjoint functors. This goes straight to the very heart of category theory.

The term “natural”, often bandied about by mathematicians, is perhaps an overloaded term (see the comments here for a recent disagreement about certain senses of the word). I don’t know the exact history of the word as used by mathematicians, but by the 1930s and 40s the description of something as “natural” was part of the working parlance of many mathematicians (in particular, algebraic topologists), and it is to the great credit of Eilenberg and Mac Lane that they sought to give the word a precise mathematical sense. A motivating problem in their case was to prove a universal coefficient theorem for Cech cohomology, for which they needed certain comparison maps (transformations) which cohered by making certain diagrams commute (which was the naturality condition). In trying to precisely define this concept of naturality, they were led to the concept of a “functor” and then, to define the concept of functor, they were led back to the notion of category! And the rest, as they say, is history.

More on naturality in a moment. Let me first give a few more examples of universal constructions. Last time we discussed the general concept of a cartesian product — obviously in honor of Descartes, for his tremendous idea of the method of coordinates and analytic geometry.

But of course products are only part of the story: he was also interested in the representation of equations by geometric figures: for instance, representing an equation as a subset of the plane. In the language of category theory, the variable denotes the second coordinate or second projection map , and denotes the composite of the first projection map followed by some given map :

The locus of the equation is the subset of where the two morphisms and are equal, and we want to describe the locus in a categorical way (i.e., in a way which will port over to other categories).

Definition: Given a pair of morphisms

their equalizer consists of an object and a map , such that , and satisfying the following universal property: for any map such that , there exists a unique map such that (any map that equalizes and factors in a unique way through the equalizer ).

Another way of saying it is that there is a bijection between -equalizing maps and maps ,

effected by composing such maps with the universal -equalizing map .

Exercise: Apply a universality argument to show that any two equalizers of a given pair of maps are isomorphic.

It is not immediately apparent from the definition that an equalizer describes a “subthing” (e.g., a subset) of , but then we haven’t even discussed subobjects. The categorical idea of subobject probably takes some getting used to anyway, so I’ll be brief. First, there is the idea of a monomorphism (or a “mono” for short), which generalizes the idea of an injective or one-to-one function. A morphism is monic if for all , implies . Monos with codomain are preordered by a relation , where

if there exists such that . (Such a is unique since is monic, so it doesn’t need to be specified particularly; also this is easily seen to be monic [exercise].) Then we say that two monics mapping into name the same subobject of if and ; in that case the mediator is an isomorphism. Writing to denote this condition, it is standard that is an equivalence relation.

Thus, a subobject of is an equivalence class of monos into . So when we say an equalizer of maps defines a subobject of , all we really mean is that is monic. Proof: Suppose for maps . Since , we have for instance. By definition of equalizer, this means there exists a unique map for which . Uniqueness then implies are equal to this self-same , so and we are done.

Let me turn to another example of a universal construction, which has been used in one form or another for centuries: that of “function space”. For example, in the calculus of variations, one may be interested in the “space” of all (continuous) paths in a physical space , and in paths which minimize “action” (principle of least action).

If is a topological space, then one is faced with a variety of choices for topologizing the path space (denoted ). How to choose? As in our discussion last time of topologizing products, our view here is that the “right” topology will be the unique one which ensures that an appropriate universal property is satisfied.

To get started on this: the points of the path space are of course paths , and paths in the path space, , sending each to a path , should correspond to homotopies between paths, that is continuous maps ; the idea is that . Now, just knowing what paths in a space look like (homotopies between paths) may not be enough to pin down the topology on , but: suppose we now generalize. Suppose we decree that for any space , the continuous maps should correspond exactly to continuous maps , also called homotopies. Then that is enough to pin down the topology on . (We could put it this way: we use general spaces to probe the topology of .)

This principle applies not just to topology, but is extremely general: it applies to any category! I’ll state it very informally for now, and more precisely later:

Yoneda principle: to determine any object up to isomorphism, it suffices to understand what general maps mapping into it look like.

For instance, a product is determined up to isomorphism by knowing what maps into it look like [they look like pairs of maps ]. In the first lecture in the Stone duality, we stated the Yoneda principle just for posets; now we are generalizing it to arbitrary categories.

In the case at hand, we would like to express the bijection between continuous maps

as a working universal property for the function space . There is a standard “Yoneda trick” for doing this: probe the thing we seek a universal characterization of with the identity map, here . Passing to the other side of the bijection, the identity map corresponds to a map

and this is the “universal map” we need. (I called it because in this case it is the evaluation map, which maps a pair (path , point ) to , i.e., evaluates at .)

Here then is the universal characterization of the path space: a space equipped with a continuous map , satisfying the following universal property: given any continuous map , there exists a unique continuous map such that is retrieved as the composite

(for the first arrow in the composite, cf. the exercise stated at the end of the last lecture).

Exercise: Formulate a universality argument that this universal property determines up to isomorphism.

Remark: Incidentally, for any space , such a path space exists; its topology turns out to be the topology of “uniform convergence”. We can pose a similar universal definition of any function space (replacing by , mutatis mutandis); a somewhat non-trivial result is that such a function space exists for all if and only if is locally compact; the topology on is then the so-called “compact-open” topology.

But why stop there? A general notion of “exponential” object is available for any category with cartesian products: for objects of , an exponential is an object equipped with a map , such that for any , there exists a unique such that is retrieved as the composite

Example: If the category is a meet-semilattice, then (assuming exists) there is a bijection or equivalence which takes the form

iff

But wait, we’ve seen this before: is what we earlier called the implication . So implication is really a function space object!

Okay, let me turn now to the notion of natural transformation. I described the original discovery (or invention) of categories as a kind of reverse engineering (functors were invented to talk about natural transformations, and categories were invented to talk about functors). Moving now in the forward direction, the rough idea can be stated as a progression:

• The notion of functor is appropriately defined as a morphism between categories,
• The notion of natural transformation is appropriately defined as a morphism between functors.

That seems pretty bare-bones: how do we decide what the appropriate notion of morphism between functors should be? One answer is by pursuing an analogy:

• As a space of continuous functions is to the category of topological spaces, so a category of functors should be to the category of categories.

That is, we already “know” (or in a moment we’ll explain) that the objects of this alleged exponential category are functors . Since is defined by a universal property, it is uniquely determined up to isomorphism. This in turn will uniquely determine what the “right” notion of morphism between functors should be: morphisms in the exponential ! Then, to discover the nature of these morphisms, we employ an appropriate “probe”.

To carry this out, I’ll need two special categories. First, the category denotes a (chosen) category with exactly one object and exactly one morphism (necessarily the identity morphism). It satisfies the universal property that for any category , there exists a unique functor . It is called a terminal category (for that reason). It can also be considered as an empty product of categories.

Proposition: For any category , there is an isomorphism .

Proof: Left to the reader. It can be proven either directly, or by applying universal properties.

The category can also be considered an “object probe”, in the sense that a functor is essentially the same thing as an object of (just look where the object of goes to in ).

For example, to probe the objects of the exponential category , we investigate functors . By the universal property of exponentials , these are in bijection with functors . By the proposition above, these are in bijection with functors . So objects of are necessarily tantamount to functors (and so we might as well define them as such).

Now we want to probe the morphisms of . For this, we use the special category given by the poset . For if is any category and is a morphism of , we can define a corresponding functor such that , , and sends the morphism to . Thus, such functors are in bijection with morphisms of . Speaking loosely, we could call the category the “generic morphism”.

Thus, to probe the morphisms in the category , we look at functors . In particular, if are functors , let us consider functors such that and . By the universal property of , these are in bijection with functors such that the composite

equals , and the composite

equals . Put more simply, this says and for objects of , and and for morphisms of .

The remaining morphisms of have the form . Introduce the following abbreviations:

1. for objects of ;
2. for morphisms of .

Since is a functor, it preserves morphism composition. We find in particular that since

we have

or, using the abbreviations,

In particular, the data is redundant: it may be defined either as either side of the equation

.

Exercise: Just on the basis of this last equation (for arbitrary morphisms and objects of ), prove that functoriality of follows.

This leads us at last to the definition of natural transformation:

Definition: Let be categories and let be functors from to . A natural transformation is an assignment of morphisms in to objects of , such that for every morphism , the following equation holds: .

Usually this equation is expressed in the form of a commutative diagram:

          F(f)
     F(c) ---> F(d)
      |         |
phi_c |         | phi_d
      V   G(f)  V
     G(c) ---> G(d)

which asserts the equality of the composites formed by following the paths from beginning (here ) to end (here ). (Despite the inconvenience in typesetting them, commutative diagrams as 2-dimensional arrays are usually easier to read and comprehend than line-by-line equations.) The commutative diagram says that the components of the transformation are coherent or compatible with all morphisms of the domain category.

Remarks: Now that I’ve written this post, I’m a little worried that any first-timers to category theory reading this will find this approach to natural transformations a little hardcore or intimidating. In that case I should say that my intent was to make this notion seem as inevitable as possible: by taking seriously the analogy

function space: category of spaces :: functor category: category of categories

we are inexorably led to the “right” (the “natural”) notion of natural transformation as morphism between functors. But if this approach is for some a pedagogical flop, then I urge those readers just to forget it, or come back to it later. Just remember the definition of natural transformation we finally arrived at, and you should be fine. Grasping the inner meaning of fundamental concepts like this takes time anyway, and isn’t merely a matter of pure deduction.

I should also say that the approach involved a kind of leap of faith that these functor categories (the exponentials ) “exist”. To be sure, the analysis above shows clearly what they must look like if they do exist (objects are functors ; morphisms are natural transformations as we’ve defined them), but actually there’s some more work to do: one must show they satisfy the universal property with respect to not just the two probing categories and that we used, but any category .

A somewhat serious concern here is that our talk of exponential categories played pretty fast and loose at the level of mathematical foundations. There’s that worrying phrase “category of categories”, for starters. That particular phraseology can be avoided, but nevertheless, it must be said that in the case where is a large category (i.e., involving a proper class of morphisms), the collection of all functors from to is not a well-formed construction within the confines of Gödel-Bernays-von Neumann set theory (it is not provably a class in general; in some approaches it could be called a “super-class”).

My own attitude toward these “problems” tends to be somewhat blasé, almost dismissive: these are mere technicalities, sez I. The main concepts are right and robust and very fruitful, and there are various solutions to the technical “problem of size” which have been developed over the decades (although how satisfactory they are is still a matter of debate) to address the apparent difficulties. Anyway, I try not to worry about it much. But, for those fine upstanding citizens who do worry about these things, I’ll just state one set-theoretically respectable theorem to convey that at least conceptually, all is right with the world.

Definition: A category with finite products is cartesian closed if for any two objects , there exists an exponential object .

Theorem: The category of small categories is cartesian closed.

Basic category theory, I

After a long hiatus (sorry about that!), I would like to resume the series on Stone duality. You may recall I started this series by saying that my own point of view on mathematics is strongly informed by category theory, followed by a little rant about the emotional reactions that category theory seems to excite in many people, and that I wouldn’t be “blathering” about categories unless a strong organic need was felt for it. Well, it’s come to that point: to continue talking sensibly about Stone duality, I really feel some basic concepts of category theory are now in order. So: before we pick up the main thread again, I’ll be talking about categories up to the point of the central concept of adjoint pairs, generalizing what we’ve discussed before in the context of truth-valued matrix algebra.

I’ll start by firmly denouncing a common belief: that category theory is some arcane, super-abstract subject. I just don’t believe that’s a healthy way of looking at it. To me, categories are no more and no less abstract than groups, rings, fields, etc. — they are just algebraic structures of a certain type (and a not too complicated type at that). That said, they are particularly ubiquitous and useful structures, which can be studied either as small structures (for example, posets provide examples of categories, and so do groups), or to organize the study of general types of structure in the large (for example, the class of posets and poset morphisms forms a category). Just think of them that way: they are certain sorts of algebraic structures which crop up just about everywhere, and it is very useful to learn something about them.

Usually, the first examples one is shown are large categories, typically of the following sort. One considers the class of mathematical structures of a given type: it could be the class of groups, or of posets, or of Boolean algebras, etc. The elements of a general such class are given the neutral name “objects”. Then, we are also interested in how the objects are related to each other, typically through transformations which “preserve” the given type of structure. In the case of sets, transformations are just functions; in the case of groups, the transformations are group homomorphisms (which preserve group multiplication, inversion, and identities); in the case of vector spaces, they are linear transformations (preserving vector addition and scalar multiplication); in the case of topological spaces, they are continuous maps (preserving a suitable notion of convergence). In general, the transformations are given the neutral name “homomorphisms”, or more often just “morphisms” or “maps”.

In all of these cases, two morphisms , compose to give a new morphism (for example the composite of two group homomorphisms is a group homomorphism), and do so in an associative way (), and also there is an identity morphism for each object which behaves as identities should ( for any morphism ). A collection of objects, morphisms between them, together with an associative law of composition and identities, is called a category.

A key insight of category theory is that in general, important structural properties of objects can be described purely in terms of general patterns or diagrams of morphisms and their composites. By means of such general patterns, the same concept (like the concept of a product of two objects, or of a quotient object, or of a dual) takes on the same form in many different kinds of category, for many different kinds of structure (whether algebraic, or topological, or analytic, or some mixture thereof) — and this in large part gives category theory the power to unify and simplify the study of general mathematical structure. It came as quite a revelation to me personally that (to take one example) the general idea of a “quotient object” (quotient group, quotient space, etc.) is not based merely on vague family resemblances between different kinds of structure, but can be made absolutely precise and across the board, in a simple way. That sort of explanatory power and conceptual unification is what got me hooked!

In a nutshell, then, category theory is the study of commonly arising structures via general patterns or diagrams of morphisms, and the general application of such study to help simplify and organize large portions of mathematics. Let’s get down to brass tacks.

Definition: A category consists of the following data:

• A class of objects;
• A class of morphisms;
• A function which assigns to each morphism its domain, and a function which assigns to each morphism its codomain. If , we write to indicate that and .
• A function , taking an object to a morphism , called the identity on .

Finally, let denote the class of composable pairs of morphisms, i.e., pairs such that . The final datum:

• A function , taking a composable pair to a morphism , called the composite of and .

These data satisfy a number of axioms, some of which have already been given implicitly (e.g., and ). The ones which haven’t are

1. Associativity: for each composable triple .
   
2. Identity axiom: Given , .

Sometimes we write for the class of objects, for the class of morphisms, and for , for the class of composable -tuples of morphisms.

Nothing in this definition says that objects of a category are “sets with extra structure” (or that morphisms preserve such structure); we are just thinking of objects as general “things” and depict them as nodes, and morphisms as arrows or directed edges between nodes, with a given law for composing them. The idea then is all about formal patterns of arrows and their compositions (cf. “commutative diagrams”). Vishal’s post on the notion of category had some picture displays of the categorical axioms, like associativity, which underline this point of view.

In the same vein, categories are used to talk about not just large classes of structures; in a number of important cases, the structures themselves can be viewed as categories. For example:

1. A preorder can be defined as a category for which there is at most one morphism for any two objects . Given there is at most one morphism from one object to another, there is no particular need to give it a name like ; normally we just write to say there is a morphism from to . Morphism composition then boils down to the transitivity law, and the data of identity morphisms expresses the reflexivity law. In particular, posets (preorders which satisfy the antisymmetry law) are examples of categories.
2. A monoid is usually defined as a set equipped with an associative binary operation and with a (two-sided) identity element for that operation. Alternatively, a monoid can be construed as a category with exactly one object. Here’s how it works: given a monoid , define a category where the class consists of a single object (which I’ll give a neutral name like ; it doesn’t have to be any “thing” in particular; it’s just a “something”, it doesn’t matter what), and where the class of morphisms is defined to be the set . Since there is only one object, we are forced to define and for all . In that case all pairs of morphisms are composable, and composition is defined to be the operation in : . The identity morphism on is defined to be . We can turn the process around: given a category with exactly one object, the class of morphisms can be construed as a monoid in the usual sense.
3. A groupoid is a category in which every morphism is an isomorphism (by definition, an isomorphism is an invertible morphism, that is, a morphism for which there exists a morphism such that and ). For example, the category of finite sets and bijections between them is a groupoid. The category of topological spaces and homeomorphisms between them is a groupoid. A group is a monoid in which every element is invertible; hence a group is essentially the same thing as a groupoid with exactly one object.

Remark: The notion of isomorphism is important in category theory: we think of an isomorphism as a way in which objects are the “same”. For example, if two spaces are homeomorphic, then they are indistinguishable as far as topology is concerned (any topological property satisfied by one is shared by the other). In general there may be many ways or isomorphisms to exhibit such “sameness”, but typically in category theory, if two objects satisfy the same structural property (called a universal property; see below), then there is just one isomorphism between them which respects that property. Those are sometimes called “canonical” or “god-given” isomorphisms; they are 100% natural, no artificial ingredients!

Earlier I said that category theory studies mathematical structure in terms of general patterns or diagrams of morphisms. Let me give a simple example: the general notion of “cartesian product”. Suppose are two objects in a category. A cartesian product of and is an object together with two morphisms , (called the projection maps), satisfying the following universal property: given any object equipped with a map for , there exists a unique map such that for . (Readers not familiar with this categorical notion should verify the universal property for the cartesian product of two sets, in the category of sets and functions.)

I said “a” cartesian product, but any two cartesian products are the same in the sense of being isomorphic. For suppose both and are cartesian products of . By the universal property of the first product, there exists a unique morphism such that for . By the universal property of the second product, there exists a unique morphism such that . These maps and are inverse to one another. Why? By the universal property, there is a unique map (namely, ) such that for . But also satisfies these equations: (using associativity). So by the uniqueness clause of the universal property; similarly, . Hence is an isomorphism.

This sort of argument using a universal property is called a universality argument. It is closely related to what we dubbed the “Yoneda principle” when we studied posets.

So: between any two products of and , there is a unique isomorphism respecting the product structure; we say that any two products are canonically isomorphic. Very often one also has chosen products (a specific choice of product for each ordered pair ), as in set theory when we construe the product of two sets as a set of ordered pairs . We use to denote (the object part of) a chosen cartesian product of .

Exercise: Use universality to exhibit a canonical isomorphism . This is called a symmetry isomorphism for the cartesian product.

Many category theorists (including myself) are fond of the following notation for expressing the universal property of products:

where the dividing line indicates a bijection between pairs of maps and single maps into the product, effected by composing with the pair of projection maps. We have actually seen this before: when the category is a poset, the cartesian product is called the meet:

In fact, a lot of arguments we developed for dealing with meets in posets extend to more general cartesian products in categories, with little change (except that instead of equalities, there will typically be canonical isomorphisms). For example, we can speak of a cartesian product of any indexed collection of objects : an object equipped with projection maps , satisfying the universal property that for every -tuple of maps , there exists a unique map such that . Here we have a bijection between -tuples of maps and single maps:

By universality, such products are unique up to unique isomorphism. In particular, is a choice of product of the collection , as seen by contemplating the bijection between triples of maps and single maps

and similarly is another choice of product. Therefore, by universality, there is a canonical associativity isomorphism

Remark: It might be thought that in all practical cases, the notion of cartesian product (in terms of good old-fashioned sets of tuples) is clear enough; why complicate matters with categories? One answer is that it isn’t always clear from purely set-theoretic considerations what the right product structure is, and in such cases the categorical description gives a clear guide to what we really need. For example, when I was first learning topology, the box topology on the set-theoretic product seemed to me to be a perfectly natural choice of topology; I didn’t understand the general preference for what is called the “product topology”. (The open sets in the box topology are unions of products of open sets in the factors . The open sets in the product topology are unions of such products where for all but finitely many .)

In retrospect, the answer is obvious: the product topology on is the smallest topology making all the projection maps continuous. This means that a function is continuous if and only if each is continuous: precisely the universal property we need. Similarly, in seeking to understand products or other constructions of more abstruse mathematical structures (schemes for instance), the categorical description is de rigeur in making sure we get it right.

For just about any mathematical structure we can consider a category of such structures, and this applies to the notion of category itself. That is, we can consider a category of categories! (Sounds almost religious to me: category of categories, holy of holies, light of lights…)

• Remark: Like “set of sets”, the idea of category of categories taken to a naive extreme leads to paradoxes or other foundational difficulties, but there are techniques for dealing with these issues, which I don’t particularly want to discuss right now. If anyone is uncomfortable around these issues, a stopgap measure is to consider rather the category of small categories (a category has a class of objects and morphisms; a small category is where these classes are sets), within some suitable framework like the set theory of Gödel-Bernays-von Neumann.

If categories are objects, the morphisms between them may be taken to be structure-preserving maps between categories, called “functors”.

Definition: If and are categories, a functor consists of a function (between objects) and a function (between morphisms), such that

• and , for each morphism (i.e., preserves domains and codomains of morphisms);
• for each object , and for each composable pair (i.e., preserves identity morphisms and composition of morphisms).

Normally we are not so fussy in writing or ; we write and for morphisms and objects alike. Sometimes we drop the parentheses as well.

If are groups or monoids regarded as one-object categories, then a functor between them amounts to a group or monoid homomorphism. If are posets regarded as categories, then a functor between them amounts to a poset map. So no new surprises in these cases.

Exercise: Define a product of two categories , and verify that the definition satisfies the universal property of products in the “category of categories”.

Exercise: If a category has chosen products, show how a functor may be defined which takes a pair of objects to its product . (You need to define the morphism part of this functor; this will involve the universal property of products.)

I. The Category of Sets

I will write a series of posts as a way of gently introducing category theory to the ‘beginner’, though I will assume that the beginner will have some level of mathematical maturity. This series will be based on the the book, Conceptual Mathematics: A first introduction to categories by Lawvere and Schanuel. So, this won’t go into most of the deeper stuff that’s covered in, say, Categories for the Working Mathematician by Mac Lane. We shall deal only with sets (as our objects) and functions (as our morphisms). This means we deal only with the Category of Sets! Therefore, the reader is not expected to know about advanced stuff like groups and/or group homomorphisms, vector spaces and/or linear transformations, etc. Also, no knowledge of college level calculus is required. Only knowledge of sets and functions, some familiarity in dealing with mathematical symbols and some knowledge of elementary combinatorics are required. That’s all!

Sets, maps and composition

An object (in this category) is a finite set or collection.

A map (in this category) consists of the following:

i) a set called the domain of the map;

ii) a set called the codomain of the map; and

iii) a rule assigning to each , an element .

We also use ‘function’, ‘transformation’, ‘operator’, ‘arrow’ and ‘morphism’ for ‘map’ depending on the context, as we shall see later.

An endomap is a map that has the same object as domain and codomain, which in this case is .

An endomap in which for every is called an identity map, also denoted by .

Composition of maps is a process by which two maps are combined to yield a third map. Composition of maps is really at the heart of category theory, and this will be evident in plenty in the later posts. So, if we have two maps and , then is the third map obtained by composing and . Note that is read ‘ following ‘.

Guess what? Those are all the ingredients we need to define our category of sets! Though we shall deal only with sets and functions, the following definition of a category of sets is actually pretty much the same as the general definition of a category.

Definition: A CATEGORY consists of the following:

(1) OBJECTS: these are usually denoted by etc.

(2) MAPS: these are usually denoted by etc.

(3) For each map , one object as DOMAIN of and one object as CODOMAIN of . So, has domain and codomain . This is also read as ‘ is a map from to ‘.

(4) For each object , there exists an IDENTITY MAP, . This is also written as .

(5) For each pair of maps and , there exists a COMPOSITE map, . ( ‘ following ‘.)

such that the following RULES are satisfied:

(i) (IDENTITY LAWS): If , then we have and .

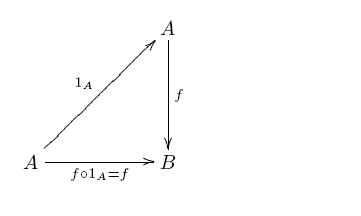
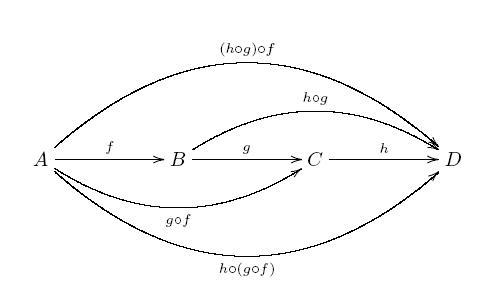
(ii) (ASSOCIATIVE LAW): If and , then we have . ( ‘ following following ‘) Note that in this case we are allowed to write without any ambiguity.

Exercises: Suppose and .

(1) How many maps are there from to ?

(2) How many maps are there from to ?

(3) How many maps are there from to ?

(4) How many maps are there from to ?

(5) How many maps are there from to satisfying ?

(This is a non-trivial exercise for the general case in which for some positive integer .)

(6) How many maps are there from to satisfying ?

(7) Can you find a pair of maps and such that . If yes, how many pairs can you find?

(8 ) Can you find a pair of maps and such that . If yes, how many pairs can you find?

Bonus exercise:

How many maps are there if is the empty set and for some ? What if and is the empty set? What if both and are empty?