I will write a series of posts as a way of gently introducing category theory to the ‘beginner’, though I will assume that the beginner will have some level of mathematical maturity. This series will be based on the the book, Conceptual Mathematics: A first introduction to categories by Lawvere and Schanuel. So, this won’t go into most of the deeper stuff that’s covered in, say, Categories for the Working Mathematician by Mac Lane. We shall deal only with sets (as our objects) and functions (as our morphisms). This means we deal only with the Category of Sets! Therefore, the reader is not expected to know about advanced stuff like groups and/or group homomorphisms, vector spaces and/or linear transformations, etc. Also, no knowledge of college level calculus is required. Only knowledge of sets and functions, some familiarity in dealing with mathematical symbols and some knowledge of elementary combinatorics are required. That’s all!

Sets, maps and composition

An object (in this category) is a finite set or collection.

A map f: A \to B (in this category) consists of the following:

i) a set A called the domain of the map;

ii) a set B called the codomain of the map; and

iii) a rule assigning to each a \in A, an element b \in B.

We also use ‘function’, ‘transformation’, ‘operator’, ‘arrow’ and ‘morphism’ for ‘map’ depending on the context, as we shall see later.

An endomap f: A \to A is a map that has the same object as domain and codomain, which in this case is A.

An endomap in which f(a) = a for every a \in A is called an identity map, also denoted by 1_A.

Composition of maps is a process by which two maps are combined to yield a third map. Composition of maps is really at the heart of category theory, and this will be evident in plenty in the later posts. So, if we have two maps f: X \to Y and g:Y \to Z, then g \circ f: X \to Z is the third map obtained by composing f and g. Note that g \circ f is read ‘g following f‘.

Guess what? Those are all the ingredients we need to define our category of sets! Though we shall deal only with sets and functions, the following definition of a category of sets is actually pretty much the same as the general definition of a category.

Definition: A CATEGORY consists of the following:

(1) OBJECTS: these are usually denoted by A, B, C, \ldots etc.

(2) MAPS: these are usually denoted by f, g, h, \ldots etc.

(3) For each map f, one object as DOMAIN of f and one object as CODOMAIN of f. So, f: A \to B has domain A and codomain B. This is also read as ‘f is a map from A to B‘.

(4) For each object A, there exists an IDENTITY MAP, 1_A. This is also written as 1_A: A \to A.

(5) For each pair of maps f: A \to B and g: B \to C, there exists a COMPOSITE map, g \circ f: A \to C. ( ‘g following f‘.)

such that the following RULES are satisfied:

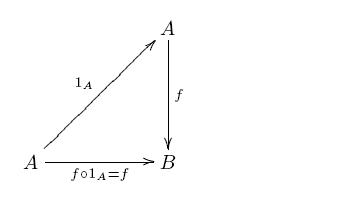
(i) (IDENTITY LAWS): If f: A \to B, then we have 1_B \circ f = f and f \circ 1_A = f.

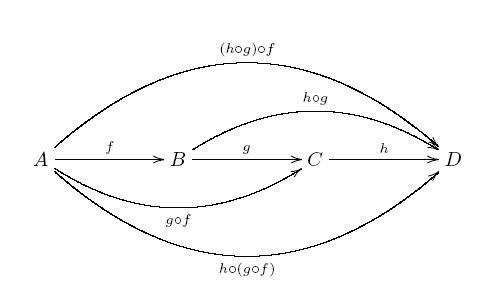
(ii) (ASSOCIATIVE LAW): If f: A \to B , \, g: B \to C and h: C \to D, then we have (h \circ g)\circ f = h \circ (g \circ f). ( ‘h following g following f‘) Note that in this case we are allowed to write h \circ g \circ f without any ambiguity.

Exercises: Suppose A = \{ a, b, c, d \} and B = \{ 1, 2, 3 \}.

(1) How many maps f are there from A to B?

(2) How many maps f are there from A to A?

(3) How many maps f are there from B to A?

(4) How many maps f are there from B to B?

(5) How many maps f are there from A to A satisfying f \circ f = f?

(This is a non-trivial exercise for the general case in which |A| = n for some positive integer n.)

(6) How many maps g are there from B to B satisfying g \circ g = g?

(7) Can you find a pair of maps f: A \to B and g: B \to A such that g \circ f = 1_A. If yes, how many pairs can you find?

(8 ) Can you find a pair of maps h: B \to A and k: A \to B such that k \circ h = 1_B. If yes, how many pairs can you find?

Bonus exercise:

How many maps f: A \to B are there if A is the empty set and |B| = n for some n \in \mathbb{N}? What if |A| = n and B is the empty set? What if both A and B are empty?