A couple of weeks ago, when Miodrag Milenkovic posed an interesting general problem in connection with POW-7, I was reminded of the “hairy ball theorem” (obviously a phrase invented during a more innocent era!), and a surprisingly easy proof of same that John Baez once told me over beers in an English pub. John is quite a good story-teller, and I wasn’t able to guess the punch line of the proof before it came out of his mouth –when it came, I was so surprised that I nearly fell off my stool! Well, I happened to run across the original source of this proof recently, and though it may be “old news” for some, it’s such a nice proof that I thought it was worth sharing.
The hairy ball theorem says: every continuous tangent vector field on a sphere of even dimension must vanish somewhere (at some point of the sphere, the tangent vector is zero). In the case of an ordinary 2-dimensional sphere, if you think of a vector at a point as a little “hair” emanating from that point, then the theorem says that you can’t comb the hairs of a sphere so that they all lie flat against the sphere: there will be a cowlick sticking straight out somewhere.
The classical proofs usually make some kind of appeal to homology theory: for example, a deep result is that the Euler characteristic of a compact manifold can be computed in terms of any continuously differentiable tangent vector field, by adding up the so-called “indices” of the vector field in the neighborhoods of critical points, where the vector field vanishes (a technical result shows there is no loss of generality in assuming the vector field is continuously differentiable). If the vector field vanishes nowhere, then the Euler characteristic is the empty sum 0; this cannot be in the case of an even-dimensional sphere, because its Euler characteristic is 2. The hairy ball theorem follows.
Some of these homology-based proofs are quite slick, but generally speaking, homology theory requires some heavy infrastructure; the question is whether a more elementary proof exists. The following “analytic” proof is due to John Milnor and uses very little machinery, basically nothing beyond advanced calculus. I will follow his exposition (American Mathematical Monthly, July 1978, pp. 521-524) pretty closely.
For the first step, suppose that we have a continuously differentiable vector field defined in a compact region of space
,
. For any real
and for
, define a function
The matrix of first partial derivatives of is
, where
denotes the
identity matrix. For
sufficiently small, the determinant of this matrix is strictly positive over all of
.
Lemma 1: If is sufficiently small, then
is a one-to-one function of
onto its image, and
is a polynomial function of
.
Proof: Since is continuously differentiable over a compact region, there is [using e.g. the mean value theorem, evidently a red rag for some people 😉 ] a Lipschitz constant
so that
We have only if
; if we assume
, this can happen only if
. So
is one-to-one for such
.
The determinant of the matrix of first partials above is of the form
where the are continuous functions in
. By the first part of the lemma, we may take
so small that
is a continuously differentiable embedding, and then by a change-of-variables formula in multivariate calculus we have that
where This completes the proof.
Next, suppose that on we have a continuously differentiable non-vanishing field
of tangent vectors. Applying the continuously differentiable map
, we assume the vector field
consists of unit tangent vectors. For each
, the vector
is thus of length
, hence
maps the unit sphere
to the sphere of radius
.
Lemma 2: For sufficiently small , the map
maps
onto the sphere of radius
.
Proof: Extend the vector field on
(and therefore also
) to the compact region between two concentric spheres,
, by homothety, i.e., put
,
for
and
. There is a Lipschitz constant
such that
for
Take , and let
be any unit vector. The function
maps the complete metric space to itself (because
and
— just use triangle inequalities), and
satisfies a Lipschitz condition
where
. By a classical fixed-point theorem,
has under these conditions a (unique) fixed point
, so that
. Rescaling
and
by the factor
, the statement of lemma 2 follows.
Now we prove the hairy ball theorem. If is a continuous non-vanishing vector field of tangent vectors on
, let
be the absolute minimum of
. By standard techniques (e.g., using the Stone-Weierstrass approximation theorem), there is a continuously differentiable vector field
such that
, and then
so that
is also non-vanishing. As above, we may then substitute
for
, i.e., assume that
consists of unit vectors.
Given , we extend
to the region
by homothety. For sufficiently small
, the map
defined above maps a spherical shell
in this region bijectively onto the shell
. Hence
maps
to the region
, and we get a dilation factor:
By lemma 1, is polynomial in
. So
must be even; therefore
admits a non-vanishing vector field only if
is odd. This gives the hairy ball theorem.
Man, what an awesome proof. That John Milnor is just a master of technique.
Just a quick note on how any of this bears on Milenkovic’s problem. He asked whether for any topological embedding of in
and any point
in the region
interior to the embedding, there exists a hyperplane
through
such that the barycenter of the
-dimensional region
coincides with
.
Under the further simplifying assumption that the barycenter varies continuously with , the answer is ‘yes’ for even-dimensional spheres. For (taking
to be the origin) we can define a tangent vector field whose value at
is the vector from
to the barycenter of
. For
even, this vector vanishes for some
, hence
coincides with the barycenter for that particular
.

19 comments
Comments feed for this article
July 22, 2008 at 11:17 am
frenchguy
It is indeed a very nice proof!
In France it has become a classic for the oral part of the mathematics Agrégation. That is, the students are randomly given a lesson in analysis and after a three-hour preparation they have to remember and provide both a fully-fledged outline of the lesson plus a choice of at least two 15 minutes long proofs, one which the jury asks to be detailed on the blackboard.
So for any analysis lesson remotely related to ‘compactess’, ‘connectedness’ or of course ‘fixed-point theorems’ the students usually choose Milnor’s neat proof as one of their choices, it fits perfectly within the 15 minutes if taking care of all the details. Here is a list I’ve just found of such classics proofs, Milnor’s is at pages 9-10.
July 22, 2008 at 3:02 pm
Todd Trimble
Très intéressante! I didn’t know any of that; that seems like quite a rigorous examination. Incomparably more than we would expect teachers to undergo here in the US. (Nice collection of topics, by the way, in that list you found.)
Funny, too, in that I’d guess this Milnor proof is probably unknown to most American mathematicians, but is apparently well-known in France!
July 22, 2008 at 9:19 pm
frenchguy
Yes funny. I’m quite sure it must be working the other way round too (stuff well-known in the US but not so in France, any thoughts?).
As for that agrégation examination, it’s indeed quite thorough but I find it a bit silly to turn Milnor’s nice proof into some cliché! I mean at the same time most of those students haven’t heard the word “homology” ever, perhaps not even “Euler characteristic”…
By the way, do you know other such elegant short proofs of interesting topological results with only undergraduate tools?
July 22, 2008 at 11:09 pm
Todd Trimble
I’m sure you’re right about the demotion of the Milnor proof to the status of cliché and rote memorization. Sort of reminds me of Muzak, which can and does appropriate any piece of music whatsoever for its limited purposes.
As for your first question, I don’t know enough about mathematics in France to say. I guess every country which has contributed substantially to modern mathematical culture has its own peculiar brand of national pride and prejudice and therefore blind spots. One of the most vituperative critics of mathematical education in France is Vladimir Arnol’d, who reserves special abuse for the abstract and formal Bourbaki tradition, which he claims has poisoned generations of students. (See this article for instance.) I’m sure he’d have an answer!
And I’m drawing a bit of a blank for your other question. The only thing that comes to mind right away is a story Gian-Carlo Rota tells in his Indiscrete Thoughts about a proof given in Dunford-Schwartz’s Linear Operators (part I, pp. 468-470) for the Brouwer fixed-point theorem, which uses only tools found in undergraduate analysis; how elegant it is seems to be a matter of controversy. Some topologists seem to think that the proof basically masks ideas made more perspicuous with a dose of De Rham cohomology. On the other hand, according to the telling by Rota, this is just one of many turf wars between those who prefer high-level abstract arguments and those who prefer direct combinatorial calculations; it’s not too hard to tell where his basic sympathies lie! We had a brief exchange about this at the n-Category Café, starting about here.
Does anyone else have insight into these matters?
July 23, 2008 at 6:49 pm
Ars Mathematica » Blog Archive » Elementary Proof of Hairy Ball Theorem
[…] at Topological Musings has posted an elementary proof of the Hairy Ball Theorem: the theorem that all vector fields on a […]
July 23, 2008 at 7:38 pm
Charles
Well, wouldn’t the Sperner’s Lemma proof of Brouwer count? After all, Sperner is a fairly basic combinatorial thing that’s pretty easy to prove itself, and it gives a pretty quick proof of Brouwer, as Walt talked about here.
July 23, 2008 at 8:14 pm
Todd Trimble
Thanks, Charles — I forgot about that. I see no reason that shouldn’t count as well.
July 24, 2008 at 4:37 pm
Todd Trimble
A reader gmailed me last night a nice letter in which he remarked on the word “homothety”: that this really derives from the French “homothétie”. In French this is pronounced as if it ended with “-cie”, as is “démocratie”, which we render in English as “democracy”. Therefore, he suggests, by phonological parallel, the correct English form really ought to be “homothecy” (he also recommends accentation on the second syllable, as in “democracy”). He observed that the suggested form “homothecy” was used not long ago by no less than Noam Elkies, in the Notices of the AMS.
So I’m passing it along for your consideration. I am still slightly undecided, if for no reason other than that the vast majority of English-speaking mathematicians write “homothety”, so there is inevitably the danger of the “huh?” factor in attempting to write otherwise. Otherwise he seems to make a reasonable point.
Incidentally — what is the etymology of this term? Surely the -thety/-thecy stem comes ultimately from the Greek, and perhaps words like “thesis” are cognates, but otherwise I don’t really know.
July 24, 2008 at 11:14 pm
Paul Shearer
I think that ‘homothety’ is preferable for three reasons:
1. It’s overwhelmingly preferred by English-speaking mathematicians.
2. The English spelling/pronunciation follows the Greek pronunciation of homo + theta.
3. Unlike homothecy, it is easily understood and remembered by any mathematician who is familiar with the meanings of the two Greek pieces:
homo = same, similar
theta = place, angle
while “-thecy” would obscure that connection.
4. If the French can change the Greek spelling and pronunciation to suit their language, why can’t English change it back to suit ours? 🙂
July 24, 2008 at 11:15 pm
Paul Shearer
I counted correctly, only 3 of these are actually reasons.
July 25, 2008 at 12:54 am
Todd Trimble
Paul, you seem to be suggesting an answer to the etymology question: homothety = same “theta” [angle], which, oddly enough, had not occurred to me. Is that in fact the derivation? Even if it were just a folk etymology, I like it!
[I’m curious about “theta = place” as well; is there something you can cite to that effect? Does this bear on why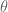 was originally chosen to denote angles (by Euler, perhaps)?]
was originally chosen to denote angles (by Euler, perhaps)?]
July 25, 2008 at 3:52 am
Paul Shearer
http://dictionary.reference.com/search?q=thetic
I don’t know if “thet(os)” can also mean angle; I overreached there.
At any rate, the etymology suggests that “homothety” should mean something like “similarly placed”, which is at least in the neighborhood of the mathematical meaning.
August 2, 2008 at 4:49 pm
John Baez
Your title suggests you’ll “analyze” the hairy ball theorem. Now I realize this was a pun. But when I first read it, I was hoping you’d analyze Milnor’s proof of this theorem and tell us what it means!
For example:
It’s very pretty, but is it fundamentally different to the usual proof, or homotopic to it in some sense? Why can this theorem, typically considered a classic application of homology theory, be done using calculus? How many other “classic applications of homology theory” can be done using calculus. When I think “calculus” and “homology theory” together, I think of de Rham theory. Does Milnor’s proof secretly involve de Rham theory?
I’ve never made much progress on any of these questions.
August 2, 2008 at 6:12 pm
Todd Trimble
I’ve only thought about it idly, so I’m in the dark too. The volume computations do suggest some connection with the top homology group obviously, but beyond that any secret connections are a bit murky to me.
I mean, the ingenious proof seems to be very geometrical (as opposed to topological) in nature — it seems to rest upon the particular standard embedding of the unit sphere in R^n. This embedding induces a number of differential-geometric structures (e.g., Riemannian metric, Levi-Civita connection, curvature, etc.) which have homological import, and I have a feeling some of this may be sneaking in through a back door.
Maybe to be just a tiny bit more explicit, there’s this theory of tubes which I really know nothing about, but which goes back to Weyl, where he apparently gives a formula for tube volumes in terms of the curvature tensor. That I suspect is secretly connected to the tube volume computations of Milnor, but for now that’s just a guess.
August 6, 2008 at 6:34 pm
Henry Wilton
Have you checked out the proof given by Thurston in “Three-dimensional Geometry and Topology” (Prop. 1.3.3)? I think it’s even more elementary, though perhaps of a more combinatorial flavour, rather than analytic.
The idea is to triangulate your manifold and put positive and negative “charges” on all the simplices, depending on whether their dimension is odd or even. What little work there is goes into showing that your triangulation can be chosen so that all the lower-dimensional faces are transverse to the non-zero vector field. Now use your vector field to “nudge” the charges into the interiors of the top-dimensional faces. A simple count shows that total charge in each face is zero – and so the Euler characteristic has to be zero too.
I agree, Milnor is a technical genius, and his proof is very slick. But as with many technically elegant proofs, the result ends up seeming somewhat mysterious, to me at least. Thurston gives a really clear idea of “why” it’s true.
August 6, 2008 at 7:55 pm
Todd Trimble
Henry, my copy of that remarkable book (which I’ve read only very selectively) has gone AWOL, but I’ll check it out when I find it — thanks for bringing it to my attention.
It would be nice if someone came along and showed how to “nudge” one one of these proofs into another by a kind of “proof-theoretic homotopy”, to put it impressionistically.
August 6, 2008 at 10:52 pm
thecooper
Todd, I wonder if that idea could be taken more literally. That would be fantastic. One of my profs used to refer to a diagram commuting as a homology.
As I recall, there’s a bit of one proof of the homotopy invariance of Morse-Bott homology where you draw a diagram, and then do Morse theory on the diagram you just drew.
On a somewhat separate note, it’s one of my longterm goals to collect a bunch of proofs by contradiction, and then publish a book where they’re all reduced to the contradiction 1=0. The Hairy Ball Theorem is a pretty good intermediate step, if you can cook up an appropriate vector field. Maybe I’ll put in a Hairy Ball chapter.
September 7, 2008 at 3:07 pm
The Hairy Ball Theorem « OU Math Club
[…] The Proof: The Hairy Ball Theorem was first proved by Brouwer in 1912. You can see the original paper here. Look for Satz 2 on page 112. In fact, if you read closely, you’ll notice that actually Brouwer proves the Hairy Ball Theorem for any sphere which as an even dimension. So dimension 2 is just one case of the more general result. The proofs most people see involves some heavy duty algebraic topology and most people don’t learn that until graduate school. However, it turns out that there was a proof given by Milnor in the 1970’s which uses only clever undergraduate analysis. A nice explanation of it is given here. […]
March 4, 2012 at 7:10 pm
Brouwer不动点定理的初等证明 « The Other Side of Moon
[…] Analyzing the hairy ball theorem […]