1. Notions of Set Theory
Artin introduces a concept that is referred to as the canonical factoring of a map (function). The basic idea is that any function can be factored into three functions
and
in a somewhat unique way:
, where
is onto,
is a bijection, and
is an injection. The construction of these three functions is done in a canonical, or natural, way that doesn’t require the use of objects outside the domain and/or range of
.
Let be some non-empty set. If
is a function from
into a set
, then we write
.
Suppose and
. Then, we can form a composite function
defined by
for all
. The associative law holds trivially for composition of functions.
Further, if , then the set of all the images of elements of
, denoted by
, is called the image of
. In general,
. We call the function
onto whenever
.
Now, let us partition the set into equivalence classes such that
are in the same equivalence class iff
. This partition is called the quotient set and is denoted by
.
To illustrate, suppose and
. Also, let
such that
and
. Then, the quotient set,
.
We construct now a function that maps each
to its equivalence class. It can be verified that
is onto. So, taking the above example, we have
,
,
and
.
Next, we construct a function where each element (which is an equivalence class) of
is mapped to a
where each
is the image of the members of the equivalence class. Recall that
are in the same equivalence class iff
. Therefore,
is one-to-one and onto. Continuing with our above example, we have
,
and
.
And, finally, we construct a trivial function where
for each
. Note that
is not an identity because it maps a subset,
, into a possibly larger set,
, i.e.
is an identity iff
is onto. In general,
is one-to-one and into (i.e. an injection.)
Thus, if , we note that
for every
.
And, so,
.
Once again, is onto,
is a bijection, and
is an injection.
It looks like it doesn’t make much sense to factor the way we did above, but we will explore more of this with respect to group homomorphisms in my next post.

24 comments
Comments feed for this article
March 8, 2008 at 5:23 pm
John Armstrong
This is a general fact for any category with a zero object, kernels, and cokernels, as I discuss here.
March 8, 2008 at 5:35 pm
Vishal
Thanks for that piece of info! I will surely go through it when I begin learning category theory myself. What is your opinion of Conceptual Mathematics: A First Introduction to Categories? That’s the only book on category theory I could get hold of from the library that was easy enough to read.
Would you recommend any other introductory book in particular?
March 8, 2008 at 9:42 pm
Andreas D.
Vishal,
congratulations for your enthusiastic and clear post.
Finding a reference like Artin’s wonderful but not particularly fashionable book
is a testimony to your fine mathematical taste.
And giving a specific example is an excellent idea: I don’t think professors do that usually, and they are wrong !
Cheers, A.D.
March 8, 2008 at 10:13 pm
John Armstrong
There’s a lot out there. MacLane is sort of the gold standard, but he doesn’t go into some fine detail. Herrlich & Strecker is another good one with more detail, but I think it loses sight of how the things are used.
Of course, I’ve had a number of people comment that they’re sending their students to read my coverage…
March 9, 2008 at 6:36 am
Vishal
Andreas,
Appreciate your comments! 🙂
Indeed, reading Artin has been an eye-opening experience for me.
March 17, 2008 at 2:36 am
Todd Trimble
I’d like to make a few categorical comments, partially in response to what John wrote above.
Vishal’s post is all about the image factorization of a function f: X –> Y, and the various steps that Vishal describes, although expressed in the language of set theory, definitely cry out for categorical generalization, as John intimated.
For example, consider the construction of the onto function. Here, what Vishal did is first form a certain equivalence relation on X based on the function f: the set E of pairs (x, x’) such that f(x) = f(x’). In category-speak, that set E is the pullback of the diagram X –> Y <– X where both arrows are f. That pullback consists of two arrows X <– E –> X, where the first arrow maps the pair (x, x’) to the first component x (i.e., is the first projection map p_1), and the second maps (x, x’) to the second component x’ (the second projection p_2). The pullback formed in this way is called the kernel pair of f.
Then what Vishal did is pass to the set of E-equivalence classes, sometimes denoted X/E. The onto function we are after is a map X –> X/E which sends an element x to its equivalence class [x]. In the language of categories, this map X –> X/E is the coequalizer of the two projection maps from E to X. It means that given any map g: X –> C such that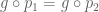 , there exists a unique map h: X/E –> C such that g is the composite of X –> X/E followed by h. This applies in particular to the case where g is the original function f: X –> Y, and so voila! we’ve factored f as X –> X/E followed by a uniquely determined map X/E –> Y. In the nicely behaved category of sets that we’re dealing with here, this map X/E –> Y is injective and can be identified (up to isomorphism) with the smallest subset through which f factors. That in a categorical nutshell is the image factorization.
, there exists a unique map h: X/E –> C such that g is the composite of X –> X/E followed by h. This applies in particular to the case where g is the original function f: X –> Y, and so voila! we’ve factored f as X –> X/E followed by a uniquely determined map X/E –> Y. In the nicely behaved category of sets that we’re dealing with here, this map X/E –> Y is injective and can be identified (up to isomorphism) with the smallest subset through which f factors. That in a categorical nutshell is the image factorization.
The technical term for categories in which such image factorizations exist and “behave well” are called regular categories. John’s comment is pointing roughly in the direction of the fact that categories in which you can take kernel pairs and coequalizers, and for which the operation of taking coequalizers is “stable under pullback” (I won’t explain this, but it’s what I meant above by “behaves well”), is regular. Unfortunately, Mac Lane’s book, which is my favorite intro to category theory, doesn’t get into the topic of regular categories. The only book I know which has pretensions to being an intro to category theory, and which has this topic, is Paul Taylor’s Practical Foundations of Mathematics. (It’s an interesting and very rich book, but I wouldn’t recommend it as a first exposure to category theory.)
But I have some responses to John’s comment. For one thing, most categories for which one could expect a good image factorization system lack zero objects (for instance, the category of sets!), so to my mind the business of zero objects slightly misses the point. But even when zero objects do exist, the notions of kernel and cokernel in the sense which I think was developed in the UM posts (where e.g. the kernel of f: X –> Y is the equalizer of f and the zero map from X to Y) are not quite the right notions with which to discuss image factorizations in general. For that to work well, I think you’d probably need to be able to reconstruct the kernel pair (the equivalence relation) from the kernel — that’s fine in the context of say Ab-enriched categories (where f and g are congruent if f – g factors through the kernel), but not for say categories enriched merely in commutative monoids, or for that matter say the category of pointed sets. So you gotta be a little careful. Finally, even if you switch from kernels and cokernels to kernel pairs and cokernel pairs, you still have to be careful: the recipe described above doesn’t always work. For example, in the category of topological spaces (or pointed topological spaces, if you want a zero object), the map X/E –> Y described above will not necessarily coincide with the smallest subspace through which f: X –> Y factors: set-theoretically it’s fine, but the topologies may differ (a simple example is where f is the identity function on X, where the domain is given say the discrete topology, and the codomain some weaker topology). So existence of the appropriate limits and colimits alone is generally not enough to do what you want.
[Apologies for such a technical comment.]
March 17, 2008 at 2:42 am
Todd Trimble
Argh. My post had an html goof-up: in the middle of the third paragraph, that should read “That pullback consists of two arrows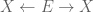 …”. [fixed] My apologies.
…”. [fixed] My apologies.
March 17, 2008 at 5:32 am
Vishal
Todd,
Your (technical) comment is one of the best I have received so far on this blog. What’s more, it is enlightening. I will be sure to study category theory during this summer seriously when I will have more time. Your comments above are very valuable to me.
Once again, thank you.
March 17, 2008 at 12:53 pm
Todd Trimble
You’re welcome, and thanks for the feedback! I should also say that I don’t want to come off as too critical of the UM’s remark: after all, he’s been doing a fine job in spreading the good categorical word, and I find his blog colorful and erudite.
I think I misdirected you in the correction I wanted to make above. Here is how that third paragraph should have read:
“For example, consider the construction of the onto function. Here, what Vishal did is first form a certain equivalence relation on X based on the function f: the set E of pairs (x, x’) such that f(x) = f(x’). In category-speak, that set E is the pullback of the diagram X –> Y <– X where both arrows are f. That pullback consists of two arrows X <– E –> X, where the first arrow maps the pair (x, x’) to the first component x (i.e., is the first projection map p_1), and the second maps (x, x’) to the second component x’ (the second projection p_2). The pullback formed in this way is called the kernel pair of f.”
March 17, 2008 at 1:49 pm
John Armstrong
Todd: good points. I didn’t mean to say that I was giving necessary conditions.. only sufficient ones.
March 17, 2008 at 2:12 pm
Vishal
Todd,
I am sorry for not editing the 3rd paragraph properly. I misread your directions earlier. I have fixed it now.
March 17, 2008 at 10:21 pm
Todd Trimble
John: actually I was also expressing skepticism about the sufficiency. I wish I had a convincing counterexample, but here is one thing which I think would be difficult to prove under your conditions: let X –> X/E be the coequalizer of the kernel pair of f: X –> Y, and let h: X/E –> Y be the corresponding map in the factorization of f; then how do you prove h is monic? (According to Barr, it isn’t always true, but I don’t have a counterexample to hand.)
You can prove this under the additional assumption that the pullback of a regular epimorphism is an epimorphism (an epimorphism is regular if it is the coequalizer of some parallel pair). As I say, the standard notion in this area is that of a regular category: a finitely complete category with coequalizers in which the pullback of a regular epi along any morphism is a regular epi. These are the categories which admit a decent calculus of relations. The reason I mentioned Top and Top_* is that these are standard examples of categories which aren’t regular.
March 18, 2008 at 1:12 pm
Anonymous
So what is the benefit of using category theory as the basis for all mathematics as opposed to set theory?
March 18, 2008 at 4:08 pm
Todd Trimble
One could also turn the question around: what is the benefit of using set theory as a basis of mathematics (as opposed to say category theory)? An untold number of trees have been sacrificed to the cause of addressing such questions, and fierce debates have ranged all over the Internet (look for example through the archives of the list FOM [Foundations of Mathematics] around 1997-1998). And they rage on still.
I’ll just say a few words on this from the POV of a category theorist. As you may know, when people talk about set theory as a foundations, they often have in mind what is known as Zermelo-Fraenkel set theory with the Axiom of Choice, a first-order theory of a binary predicate called “membership”. One of the primary historical sources of this theory was Zermelo’s careful analysis of what precisely lay behind the claim, rooted in the work of Cantor and others, that the real numbers could be well-ordered. About a century ago, this claim was considered highly controversial, partly because it is something completely impossible to visualize! In response, Zermelo carefully specified a set of exact axioms on which a precise proof could be based, including of course the crucial axiom of choice, and thus “Zermelo set theory” was born. (Fraenkel’s own contribution, the so-called Axiom of Replacement, came later.) Zermelo’s axioms were of course powerful enough to permit a construction of the real number system, and over the course of time, together with the elaboration and perfection of the predicate calculus, it became clear that, at least in principle, virtually all the structures and theorems considered in mathematics could be codified in the theory ZFC.
Most mathematicians treat that fact (and it is a pretty well-established fact) as a given, without necessarily ever working directly with ZFC at all — as a theory of the membership relation, it is actually of a terrible combinatorial complexity. I think in practice, the “axiomatics” of working mathematicians, when they think in such terms, is much more local in character; there is a kind of naive assurance in the dogma that any such axiomatics could ultimately be encoded in the language of ZFC, but to actually do so would be completely alien to normal practice, and hardly likely to be productive or to aid in the advancement of mathematics. Perhaps you can think of ZFC as a kind of “machine language” (and perhaps there is some interest in using such a language for computer-generated mathematics or automated theorem proving, although I tend to think there are far more efficient languages available) — the point being that serious “programmers” or theorem provers, that is, mathematicians, tend to think in terms of higher-level languages, and not one at the machine level.
And I think this is where category theory comes in, at the level of normal practice. Getting back to the primary historical source, Eilenberg and Mac Lane introduced categories and functors not with any foundational pretensions in mind, but in order to analyze the crucial notion of “natural transformation” (what it meant for a mapping or construction to be “natural”); I think the motivating problem was actually to prove the universal coefficient theorem for Cech cohomology. The theory actually lay more or less dormant (despite some early work on what developed into abelian categories, and some early recognition of universal mapping properties) for about a dozen years, when the truly revolutionary discovery of adjoint functors (due to Daniel Kan) came about. During the late fifties and throughout the sixties, the simplicity and power of this basic tool in the conceptual unification of basic mathematical ideas became manifest; I don’t think there’s anything quite like it in set theory. (Just to give one example: all of the operations in predicate logic: the propositional connectives, the quantifiers, etc., are all instances of adjoint functor relationships — a crucial and profound observation of Lawvere.)
I actually think the comparison of set theory and category theory is a bit like apples and oranges. I don’t think of category theory so much as a single monolithic theory as ZFC is, but rather as a box of simple and precise tools which in fact are more adaptable to the local axiomatics of practicing mathematicians. It is wonderful and in fact liberating to be able to see that the constructions used in algebraic topology are comparable to those used in mathematical logic, when seen for example as manifestations of basic categorical ideas. So: “category theory” affords a kind of conceptual unification of great big chunks of mathematics, with consequent advantages in learning and comprehending mathematics.
I don’t think it is too partisan to say that the tools of category theory are far, far more important to the daily practice and understanding of modern mathematics than is ZFC, for these reasons.
Now: it is true that some propose topos theory as an alternative to ZFC as a “foundations” for mathematics. I honestly think this is misleading, or at least is subject to a misunderstanding of the role of category theory in mathematics. But an awful lot could be said on that score.
So I’ll leave it at that for now, and I hope this has been a little bit clarifying.
March 18, 2008 at 4:26 pm
Todd Trimble
Reading my last comment over, I can see how some of it would come off as tendentious. Oh well. Maybe it will spur some interesting further discussion.
March 19, 2008 at 12:47 am
#John
Todd said: So: “category theory” affords a kind of conceptual unification of great big chunks of mathematics, with consequent advantages in learning and comprehending mathematics
in which case ought it not be taught to very young mathematics students, say at the high school level?
Secondly I would ask, what are the ‘ultimate’ goals in category theory? What are the problems within it?
March 19, 2008 at 2:39 am
Todd Trimble
#John: it really depends. Given the current norms of education in the US (where I live), it doesn’t seem feasible to teach it at the high-school level unless to highly gifted and motivated students. Put it this way: if you have some students at that age who are ready and willing to learn some abstract algebra or topology, then I don’t see why you couldn’t teach them some category theory as well.
On the other hand, the book Conceptual Mathematics: A First Introduction to Categories, mentioned in a comment above by Vishal, was apparently based on lectures given to a class of first-year college students.
In the normal scheme of things, it makes sense to expose students to categorical principles starting in upper-level undergraduate courses. What I’ve often done myself as a teacher is teach categorical ways of thinking without even mentioning the word “category”. To give just one example: in introductory analysis or topology courses, students need to gain some facility in manipulating and calculating with sets (unions, direct images, inverse images, etc.), and there just a few categorical ideas at an informal level, e.g. universal mapping properties just at the level of posets, go a long way in organizing the material and guiding calculations.
The “ultimate goals” question has no simple answer, because category theory is awfully spread out, and really its life blood lies in its applications to the rest of mathematics (and so the goals of categorist X are largely intertwined with the particular field of application under study). But, for example, the area of higher-dimensional categories is largely undeveloped and conjectural at this point: internally, there is the problem of comparing and unifying the various proposed definitions and taming their complexity in terms of “partial strictifications”, and externally there are problems like the “homotopy hypothesis” and the “tangle hypothesis” — you might like to try following the links here to get a better idea of what some of this is about.
[Apologies to Vishal for the highjacking of his thread.]
March 19, 2008 at 3:59 am
John Armstrong
I second Todd’s reply to #John. The big problem here is that category theory requires a certain level of sophistication to follow. I’d say what it unifies (as Todd put it before) is the mathematics after the standard introductory calculus-etc sequence, and so it could feasibly be taught at that point as a lead-in to abstract algebra, topology, and so on. Notice that in my expository line I went through all that category theory before topology, but after a little abstract algebra to build up some level of intuition and to give me some categories to work with.
March 19, 2008 at 10:32 am
Vishal
Todd,
I have thoroughly enjoyed reading every comment of yours on this thread. I am mostly silent because I don’t have anything significant to say on this topic. Please do continue the discussions in any direction(s) you want. All this is really invaluable to me and, I am sure, others too. At least, I am seriously considering studying introductory category theory on my own, now.
March 19, 2008 at 10:41 pm
Todd Trimble
Vishal,
Great! I say why not start now, if the mood strikes! And certainly self-study is feasible — I myself learned category theory on my own, just by reading good stuff and thinking a lot about it.
Maybe I will add some more words to my last long comment on set theory vs category theory, because that comment was a bit on the impressionistic side I think.
In the first place, I don’t think the debate is about which is conceptually prior: set or category; clearly, the naive concept of set or collection precedes the more complicated concept of category. No, the actual Lawverean criticism of set theory as ensconced in the formal theory of ZFC is that it promotes a conception of “set” as a member of a cumulative hierarchy: a set has elements which may itself have elements which may itself have… you get these iterated membership chains. According to Lawvere, that’s a kind of phony conception of what a set “is”. In actual mathematical practice, no one cares what the elements of a set “really are” (whether themselves sets or something else) — what we care about in practice are the “operational” aspects: the possibility of identifying or distinguishing two given elements of a specified set, or detecting whether a given element belongs to a given subset — never mind what the elements are in substance! No normal mathematician thinks of elements of a structure as having membership trees growing off of them, as suggested by the formal picture of ZFC!
If the ZFC conception is morally “wrong” or introduces extraneous mathematical irrelevancies, it is then natural to enquire what aspects of naive set theory we do retain in normal mathematical practice, and whether those can be effectively formalized. The categorical answer is that we want those aspects which guarantee a rich supply of operations with which to construct new sets from old ones, and these constructions tend to be describable (up to isomorphism) by universal properties, which are mathematically more relevant than descriptions based on membership relations. For example, to represent things like 3-dimensional space, we would like our sets to admit an operation of taking a cartesian product of two given sets X and Y. In Zermelo-Fraenkel set theory, this may be accomplished using an axiom of pairs which produces, given elements x and y, an element z whose elements are precisely x and y (denoted {x, y}), and then define the ordered pair (x, y) as say the pair {x, {x, y}}. Then by other axioms, it is possible to form the set of all ordered pairs. But, the only mathematically relevant property of the cartesian product is the universal property, and so in categorical set theory we appeal directly to an axiom: given sets X and Y, there exists a set Z equipped with “projection” maps Z –> X, Z –> Y which is universal: given any other set A together with a pair of maps A –> X, A –> Y, there exists a unique map A –> Z whose composites with the projections yield the given pair.
And so it is with all the basic operations we need: the important issue is not ontological (what sets and their elements “really are”), but operational (what they are used for), and the relevant operations are describable by means of universal properties. This is true of power sets, of loci of equations, of cut-and-paste constructions (colimits), etc. etc. This then is the categorical view on sets.
A topos is a category satisfying some axioms of set theory expressed in terms of universal properties, and so categorists sometimes think of a topos as consisting of “set-like objects” — but the notion turns out to be an expansion of the ordinary view on sets: it can accommodate things like sets conceived as varying in time and space, or varying over algebras — it’s a pretty wide notion. It is however fascinating that we can apply ordinary set-theoretic reasoning in all these cases, with the important caveat that the logic applied is generally intuitionistic. (It is often possible, in Lawvere’s language, to “freeze the variation” and get objects more closely resembling the more usual notion of “constant set” whose “Platonic ideal” is that of a set which doesn’t change over time or vary in some other way, but the POV of topos theory is generally to contemplate a less rigid notion of set.)
Can we speak of “elements” in categorical set theory? Certainly: one can define an element of X, or a constant of X, simply as a morphism x: 1 –> X where 1 is terminal. (Put that way, notice it doesn’t even make sense to ask “what are the elements of an element?”!)
In the more rigid conceptions of “set”, a set X may be determined by its elements in the categorical sense, that two morphisms f, g from X to Y are distinct iff they are distinct at some element x (i.e. there exists x: 1 –> X such that the composites fx and gx are distinct). When that is the case for all X, we say the category of sets is “well-pointed”. But most toposes do not have this property.
In summary, the world of ordinary “naive set theory” is a special case of topos theory: categorically, ordinary sets constitute a well-pointed topos with exactly two truth values. The empirical claim is that practically all of “core mathematics” can be expressed without essential distortion in the theory of such a topos. I would be interested to see this claim subjected to the “torture test” — a possible sticking point would be some essential use of the Axiom of Replacement in some core result (and of course “core mathematics” is a vague term — I mean for example that one should be able to express the contents of a course in real analysis, complex analysis, differential geometry, etc. wholly within this framework). Typically Replacement is used to prove certain results of a meta-mathematical character; I wonder if or how it rears its ugly head in more mainstream mathematics.
I hope it is clear from this description that categorical set theory is not to be considered “at odds” with the usual naive set theory of practicing mathematicians. The claim is that it more faithfully reflects actual practice than ZFC does, and has also led to an expansion of how we think about sets in the first place.
March 20, 2008 at 1:24 am
Vishal
Indeed, in ZFC, the “usual” way of defining ordered pairs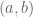 is by writing
is by writing
 .
.
Apropos the above definition of ordered pairs, Halmos, in his book Naive Set Theory, notes the following:
“It is easy to locate the source of the mistrust and suspicion that many mathematicians feel toward the explicit definition of ordered pairs given above. The trouble is not that there is anything wrong or anything missing… The trouble is that the concept has some irrelevant properties that are accidental and distracting. The theorem that iff
iff  and
and  is the sort of thing we expect to learn about ordered pairs. The fact that
is the sort of thing we expect to learn about ordered pairs. The fact that  , on the other hand, seems accidental; it is a freak property of the definition rather than an intrinsic property of the concept.”
, on the other hand, seems accidental; it is a freak property of the definition rather than an intrinsic property of the concept.”
On the other hand, the categorical construction of ordered pairs looks much more natural!
March 20, 2008 at 5:44 pm
John Armstrong
No, you’re missing the point here. Don’t worry, though — everybody does at first.
In category theory we don’t construct ordered pairs. We define the categorical product to be a set and two functions, satisfying a certain universal property. We can show that if any set fits this definition, then it’s unique (up to unique isomorphism). Any set with two maps that satisfies this condition is just as good as any other, whether its elements are pairs, chairs, or shades of blue.
But then we come back and show that there exists at least one set (with two maps) that satisfies the universal condition: the set of ZFC-defined pairs.
March 29, 2008 at 8:05 pm
Vishal
Indeed, after having gone through the definition of a product of two objects and
and  in a category
in a category 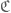 , I see now where I made a mistake in mentioning that ordered pairs are categorically “constructed.” Thinking in terms of morphisms is going to take some time, it seems!
, I see now where I made a mistake in mentioning that ordered pairs are categorically “constructed.” Thinking in terms of morphisms is going to take some time, it seems!
March 30, 2008 at 5:03 pm
#John Smith
But vishal, why can’t we just define ordered pair as a bijection from {a,b) to itself?