I wasn’t keeping well – nothing too serious though – over the past few days, and going through a slight bout of depression doesn’t help very much either. I think I have recovered now. During such periods, it helps (I think) to keep the mind busy over some light puzzle(s) just so it remains active and healthy. Anyway, let me pose a nice puzzle that I first read in a book by Yakov I. Perelman many years ago, and I invite you to post your solutions. In keeping with the spirit of the puzzle, I will stick to Russian names and currency, even though the names I use below aren’t the same as the ones used in the original puzzle.
Anna, Bogdana and Calina are three young mathematicians who decide, one fine day, to go camping. During camping, in the evening they light a campfire to keep themselves warm and also to discuss (what else?) mathematics! Anna and Bogdana had brought with them three and five logs of wood, respectively, but unfortunately, Calina forgot to bring any log of wood with her. Instead, she gave 8 rubles to the other two girls. If Calina didn’t want any money back and if all the eight logs of wood were used for building the campfire, how should Anna and Bogdana distribute the 8 rubles between themselves in a fair manner?
Todd and Vishal's blog 
25 comments
Comments feed for this article
April 13, 2008 at 11:46 pm
John Smith
in the ratio 5:3 to Bogdana and anna respectively?
April 13, 2008 at 11:49 pm
Vishal Lama
That’s what one would instinctively think the answer would be! However, it is not. Can you see why?
April 14, 2008 at 12:18 am
John Smith
no I can’t?
April 14, 2008 at 1:15 am
Vishal Lama
If Anna and Bogdana had got those 8 rubles and if they had *not* used the campfire, then surely the ratio of money the two of them would get is 3:5 ratio. But, the thing is Anna and Bogdana both did use the campfire, and this changes our final answer!
April 14, 2008 at 5:03 am
Anonymous
The Bogdana gets 7 Rubles for 5 logs and anna gets 1 Ruble for 3 logs.
April 14, 2008 at 11:59 am
John Smith
But why?
and what difference does it make if they used the campfire or not?
April 14, 2008 at 2:35 pm
John Armstrong
Treat the campfire as a good to be traded.
A puts in 3 logs, B puts in 5 logs, C puts in 8 rubles.
A gets 1/3 fire and X rubles, B gets 1/3 fire and Y rubles, C gets 1/3 fire and 0 rubles.
So 8 rubles are “worth” 1/3 of the fire. Plugging this into the A and B trades we see that
(8+X) rubles = 3 logs
(8+Y) rubles = 5 logs
thus
(40+5X) rubles = 15 logs = (24+3Y) rubles
and we have the system
5X – 3Y = -16
X + Y = 8
7X – Y = 0
Y = 7X
so B gets 7 times what A gets. Luckily(!) 8 = 1+7
April 22, 2008 at 3:59 pm
JC
John Armstrong’s explicit mention of the “worthiness” of the rubles shows us the practical aspects of this amusing puzzle (which may come in handy not only when there are companions who forget to bring their own logs…(for example, a visiting professor having a city tour with a group of local undergraduates)): One may substitute the logs with any other kind of currency (provided that the exchange rate is accepted by all people involved, of course!).
In our original case 1Logs=3Rubles, so that Anna and Bogdana had 15(=7+8 ) and 9(=1+8 ) rubles, respectively. And it is generalisable for a group of n people…
April 28, 2008 at 11:54 pm
Aaron F.
“Treat the campfire as a good to be traded…. A gets 1/3 fire and X rubles, B gets 1/3 fire and Y rubles, C gets 1/3 fire and 0 rubles.”
I don’t buy it! If Anna is sitting by the fire and Calina comes and joins her, Anna does not suddenly have less access to the fire. The question of how the number of campers affects the utility each camper gets from the fire can have a significant impact on the answer to the problem.
In fact, it’s not hard to imagine a situation where Anna and Bogdana should be paying Calina, rather than the other way around! Suppose the following:
1. The campers are interested primarily in staying warm.
2. Heat flows from the fire to the campers mostly in the form of radiation.
3. There is enough room for all three campers to sit comfortably close to the fire.
Each camper recieves radiation in two ways: directly from the fire, and indirectly due to reflection off the other campers. Since there is enough room for all three campers to sit comfortably close to the fire, the amount of direct radiation recieved by each camper does not depend on the number of campers. The amount of reflected radiation recieved by each camper, however, increases as the number of campers increases! Anna and Bogdana recieve a net gain in heat from Calina’s presence, so they should be willing to pay Calina to sit with them.
May 10, 2008 at 2:20 pm
rbnn
Why is it that whenever someone posts a puzzle on the Internet, someone has to invent some preposterous hypothesis to make its assumptions nonsensical?
May 14, 2008 at 3:45 am
Paul Shearer
The principle that the fire is a commodity makes sense, and once that is assumed John Armstrong’s solution clearly follows. But it is still hard to understand intuitively why the 5:3 solution is wrong. It makes more sense when you think of a more extreme case. Suppose B holds 8-s logs and A holds s logs, where s is a small number (s stands for a sliver of a log!). It definitely seems unfair for B to get 8-s rubles and A gets s rubles; A is getting the fire practically for free (literally for free if s=0).
The funny thing is, only at an economist’s campout would anyone dare propose the 7:1 solution to the original 5:3 problem. The fairness principle is too abstract, and relatively few people (as a fraction of the generally innumerate masses) could correctly formulate and solve the resulting linear system. I think if the 5 log girl proposed the 7:1 rate to the other girls, they would both vote against it as unfair.
May 14, 2008 at 3:56 am
Vishal Lama
Paul,
You raise a valid point, as in the 7:1 solution seems rather counter-intuitive!
However, let me throw back what you wrote in the first paragraph of your comment above. Suppose, Calina did not use the fire at all but still decided to give 8 rubles to the other two girls. Then, how would/should those two girls distribute the money between themselves given that one of them contributed 5 logs of wood and the other 3 logs?
May 14, 2008 at 4:36 am
Paul Shearer
They should treat the 8 rubles as an act of charity and split it 50-50 (that is, ignore it essentially). Then they start bargaining over how much Anna should pay Bogdana for the right to 1/2 a fire.
Unlike the original puzzle, the “market price” for a share of the fire has not been agreed upon yet. In the original, Anna and Bogdana implicitly accepted Calina’s 8 rubles as the fair market price for a 1/3 fire share. But with her out of the picture, the girls must agree on the price of a fire share. That will depend on how rich each one is and how cold 🙂
May 14, 2008 at 5:13 am
Vishal Lama
Oops! My bad. That is not what I intended to ask. Sorry about that. Let me ask the correct question.
Suppose, Anna and Bogdana give away their (eight) logs of wood to Catalina, who then alone builds and uses the fire. As usual, Catalina gives 8 rubles to the other two in exchange. Then how should those two distribute the money between themselves?
May 14, 2008 at 5:34 am
Paul Shearer
Then the ratio is 3:5 as you mentioned above. Catalina is buying 8 logs for 8 rubles, so the fair exchange rate must be 1 log/ruble.
My initial post was an attempt to retrain the gut reaction to this problem so that the wrong answer feels wrong and the right answer feels right. If 3:5 is wrong, there should be a way to make it “feel” prima facie absurd; you can feel that if you change the problem to 8-s and s.
I definitely agree now that it is more “fair” to treat the fire as a tradeable commodity, as JA does.
May 14, 2008 at 5:48 am
Vishal Lama
I definitely agree with what you just said: prima facie one should indeed “feel” that 3:5 is wrong!
Actually, there is yet another (well-known) problem which has a somewhat similar favor to the one I posed. And the “gut” answer to it is also wrong though it feels so right!
A person drives from town A to town B at a constant speed of 40 km/hr. As soon as he reaches his destination, he immediately turns back and drives toward town A. (Assume that the turning back is instantaneous!) This time he travels from town B to town A at 60 km/hr. What is his average speed during the entire journey?
The instant answer that one thinks of is 50 km/hr, which is of course wrong!
May 14, 2008 at 6:11 am
Paul Shearer
Again, a good place to apply the principle of extreme cases. Suppose we travel at light speed from A to B, then at a snail’s pace from B to A. Surely our average speed is not half light speed; for then the roundtrip would be nearly instantaneous. But we know the B-to-A leg will make the roundtrip much longer than that.
I’ll be the first to admit though, I fall for these sorts of problems nearly every time 🙂 here’s one more:
Anna and Bogdana grow up to be lovely tennis players. Anna is much better than Bogdana though, and will score a point against her p = 99.9% of the time on a given volley. Now Anna and Bogdana play a match — first to 5 points wins. Is Anna more likely to win the match with when the score is 0-1 (Anna trails), or when it is 3-3? [Forget the real rules of tennis here!]
May 14, 2008 at 8:08 am
Vishal Lama
Ok, let me see if I got this right. Suppose, Anna scores a point against Bogdana with a probability
on a given volley. Then clearly, Bogdana scores a point against her opponent with probability 
on the same volley.
Now, if Anna trails 0-1 initially, then the probability that she wins is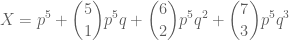
.
And, if Anna is tied 3-3 initially, then the probability that she wins is
.
Obviously, the truth of
will depend on the value of 
. But, the above two expressions are rather ugly! And, I am somewhat loathed to compute the values of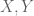 
for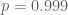 
in order to answer your question! 🙂
Btw, you wrote,
Anna and Bogdana grow up to be lovely tennis players.
That’s rather wishful thinking, don’t you think so? 😀
May 14, 2008 at 12:00 pm
Todd Trimble
Rather wishful? Well, there are quite a few hot Russian players in women’s tennis!
Here’s another way averages can be deceptive. In my car there’s a meter which computes fuel efficiency instantaneously in mpg (miles per gallon). If I let myself coast down one hill, it might read 99.9 mpg (as high as it will go); if I then hit the gas to go up another hill the same distance and it reads 7 mpg throughout, is the average efficiency more than 50 mpg? No! It’s no better than 14 mpg. Mathematically, one needs to take the harmonic mean (as in the average speed problem a few comments up).
This makes me think that if car manufacturers really want you to save fuel, they should save you mental computation by measuring gpm (gallons per mile) instead. Or, maybe even better would be gph (gallons per hour), since people generally have some idea how long routine car trips take.
May 14, 2008 at 3:38 pm
Vishal Lama
I meant, given three random Russian girls/women (in this case, Anna, Bogdana and Calina), Paul should think that two-thirds of them will be hot! That’s a rather high ratio, and hence my “wishful thinking” comment! 😀 Hmmm… but come to think of it, that ratio may not be that high, after all! Btw, my favorite is Sharapova! I wonder what Paul and your favorites are.
May 14, 2008 at 4:04 pm
Todd Trimble
Hm, we are talking about “hot” in terms of skill level, right? 😉 Either way, maybe I’ll submit my answer to topological[dot]musings[At]gmail[dot]com, as a spirited discussion could take us a little off-topic. 🙂
May 14, 2008 at 4:26 pm
Paul Shearer
oops, the algebra gets a little messy for the case I gave doesn’t it?
Let’s change the scores to 0-1 and 2-2, winner is first to 3. Then the computation is easy (once you get it into the right form!)
Note that if p is sufficiently close to 1, you should be able to make the counterintuitive result look arbitrarily absurd. Can you give a lower bound on p which guarantees that (for example) a 0-8 losing streak is better for A than a score of 9-9 in a “first to 10” game? (I do not know a good way to solve this, I just came up with it now!)
May 14, 2008 at 5:02 pm
Vishal Lama
Ok, in this case, the expressions are “nice” and the computations easy!
So, in the “winner is first to 3” case,
if Anna trails 0-1 initially, then the probability she wins is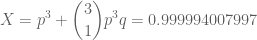
(which I got with the help of a calculator.)
And, if Anna is tied 2-2 initially, then the probability she wins is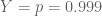
. Clearly, 
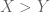. So, she has a better chance of winning when she trails 0-1 than when she is tied 2-2: a somewhat counter-intuitive result! Nice exercise!
To answer your last question, I guess finding a solution in the general case might be somewhat “helpful”. Say, the winner is one who reaches
points first, and then we find an expression for the probability of Anna winning the game when the score is 
. I am not doing it right now though! 🙂
December 27, 2010 at 11:20 am
seo discussion
nice dud cheers for every info
December 27, 2010 at 11:21 am
seo discussion
looks like you will get tons of comment this year