This is a post on “foundations of mathematics” (eek!). I was motivated to write it while I’ve been struggling to understand better certain applications of ultrafilters — namely the theory of measurable cardinals — from a point of view and language that I feel comfortable with. My original intent was to blog about that, as a kind of off-shoot of the general discussion of ultrafilters I started in connection with the series on Stone duality, and because it seems kind of cool. And I will. But this got finished first, and I thought that it would be of interest to some who have been following my category theory posts.
A lot of confusion seems to reign around “the categorical approach to foundations” and what it might entail; some seem to think it involves a “doing-away with elements” that we all know and love, or doing away with sets and supplanting them with categories, or something like that. That’s an unfortunate misunderstanding. My own attitude is pragmatic: I’m all in favor of mathematicians using ordinary “naive” (pre-axiomatic) set theory to express their thoughts if that’s the familiar and appropriate conveyance — I mean, obviously I do it myself. It’s our common heritage, learned through years of undergraduate and graduate school experience and beyond. I’m not proposing for a moment to “overthrow” it.
What I do propose to discuss is a formalized set theory which embodies this rich tradition, but which takes advantage of categorical insights honed over the decades, and which I would argue is ‘natural’ in its ease to accept formulas in naive set theory and give them a foundation true to mathematical practice; I also argue it addresses certain criticisms which I feel could be put to that hallowed foundational theory, ZFC. I should own up that this theory is not immune to criticism, a main one being that a certain amount of preface and commentary is required to make it accessible (and I don’t think category theorists have done a particularly hot job doing that, frankly).
Let’s start by putting down what we want in very simple, pragmatic terms:
- A (formalized) ‘set theory’ worthy of the name ought to realize a conception of sets as “completed collections”, and allow for the existence of enough sets and relations to fulfill the needs of working mathematicians.
This is intentionally vague. The “needs of working mathematicians” fluctuate over time and place and person. Some of the core needs would include the existence of the sets of natural numbers and real numbers, for instance. On the other hand, set theorists may have greater needs than specialists in the theory of several complex variables. For now I’ll ignore some of the deeper needs of set theorists, and try to focus on the basic stuff you’d need to formalize what goes on in your average graduate school text (to put it vaguely, again).
We will discuss two formalizations of set theory: ZFC, and Lawvere’s Elementary Theory of the Category of Sets [ETCS]. The first “needs no introduction”, as they say. The second is an autonomous category-based theory, described in detail below, and proposed by Saunders Mac Lane as an alternative approach to “foundations of mathematics” (see his book with Moerdijk). Either formalization provides fully adequate infrastructure to support the naive set theory of working mathematicians, but there are significant conceptual differences between them, centering precisely on how the notion of membership is handled. I’ll start with the more familiar ZFC.
As everyone knows, ZFC formalizes a conception of “set” as collection extensionally determined by the members it contains, and the ZFC axioms ensure a rich supply of ways in which to construct new sets from old (pairings, unions, power sets, etc.). Considering how old and well-developed this theory is, and the plenitude of available accounts, I won’t say much here on its inner development. Instead, I want to pose a question and answer to highlight a key ZFC conception, and which we use to focus our discussion:
Question: “What are the members of sets?”
Answer: “Other sets.”
This may seem innocent enough, but the consequences are quite far-reaching. It says that “membership” is a relation from the collection
of all “sets” to itself. (Speaking at a pre-axiomatic level, a relation from a set
to a set
is a subset
. So a structure for ZFC set theory consists of a “universe of discourse”
, together with a collection
of pairs of elements of
, called the membership relation.)
Why is this a big deal? A reasonable analogue might be dynamical systems. If and
are manifolds, say, then you can study the properties of a given smooth map
and maybe say interesting things of course, but in the case
, you get the extra bonus that outputs can be fed back in as inputs, and infinite processes are born: you can study periodic orbits, long-term behaviors, and so on, and this leads to some very intricate mathematics, even when
is a simple manifold like a 2-sphere.
My point is that something analogous is happening in ZFC: we have a (binary) relation from
to itself, and we get a rich “dynamics” and feedback by iterative relational composition of
with itself, or by composing other derived binary relations from
to itself. (Perhaps I should recall here, again at a pre-axiomatic level, that the composite
of a relation
and
is the subset
.)
A “behavior” then would correspond to an iterated membership chain
and there are certain constraints on behavior provided by things like the axiom of foundation (no infinitely long backward evolutions). The deep meaning of the extensionality axiom is that a “set” is uniquely specified by the abstract structure of the tree of possible backward evolutions or behaviors starting from the “root set”
. This gives some intuitive but honest idea of the world of sets according to the ZFC picture: sets are tree-like constructions. The ZFC axioms are very rich, having to do with incredibly powerful operations on trees, and the combinatorial results are extremely complicated.
There are other formulations of ZFC. One is by posets: given any relation (never mind one satisfying the ZFC axioms), one can create a reflexive and transitive relation
, defined by the first-order formula
if and only if
The “extensionality axiom” for can then be formulated as the condition that
also be antisymmetric, so that it is a partial ordering on
. If
is the membership relation for a model of ZFC, then this
is of course just the usual “subset relation” between elements of
.
Then, by adding in a suitable “singleton” operator so that
if and only if
the rest of the ZFC axioms can be equivalently recast as conditions on the augmented poset structure . In fact, Joyal and Moerdijk wrote a slim volume, Algebraic Set Theory, which gives a precise (and for a categorist, attractive) sense in which models of axiomatic frameworks like ZF can be expressed as certain initial algebras [of structure type
] within an ambient category of classes, effectively capturing the “cumulative hierarchy” conception underlying ZFC in categorical fashion.
The structure of a ZFC poset is rich and interesting, of course, but in some ways a little odd or inconvenient: e.g., it has a bottom element of course (the “empty set”), but no top (which would run straight into Russell’s paradox). Categorically, there are some cute things to point out about this poset, usually left unsaid; for example, taking “unions” is left adjoint to taking “power sets”:
if and only if
.
In summary: ZFC is an axiomatic theory (in the language of first-order logic with equality), with one basic type and one basic predicate
of binary type
, satisfying a number of axioms. The key philosophic point is that there is no typed distinction between “elements” and “sets”: both are of type
, and there is a consequent very complicated dynamical “mixing” which results just on the basis of a short list of axioms: enough in principle to found all of present-day mathematics! I think the fact that one gets such great power, so economically, from apparently such slender initial data, is a source of great pride and pleasure among those who uphold the ZFC conception (or that of close kin like NBG) as a gold standard in foundations.
My own reaction is that ZFC is perhaps way too powerful! For example, the fact that is an endo-relation makes possible the kind of feedback which can result in things like Russell’s paradox, if one is not careful. Even if one is free from the paradoxes, though, the point remains that ZFC pumps out not only all of mathematics, but all sorts of dross and weird by-products that are of no conceivable interest or relevance to mathematics. One might think, for example, that to understand a model of ZFC, we have to be able to understand which definable pairs
satisfy
. So, in principle, we can ask ourselves such otherwise meaningless gibberish as “what in our model and implementation is the set-theoretic intersection of the real number
and Cantor space?” and expect to get a well-defined answer. When you get right down to it, the idea that everything in mathematics (like say the number
) is a “set” is just plain bizarre, and actually very far removed from the way mathematicians normally think. And yet this is how we are encouraged to think, if we are asked to take ZFC seriously as a foundations.
One might argue that all expressions and theorems of normal mathematics are interpretable or realizable in the single theory ZFC, and that’s really all we ever asked for — the details of the actual implementation (like, ‘what is an ordered pair?’) being generally of little genuine interest to mathematicians (which is why the mathematician in the street who says ZFC is so great usually can’t say with much specificity what ZFC is). But this would seem to demote ZFC foundations, for most mathematicians, to a security blanket — nice to know it’s there, maybe, but otherwise fairly irrelevant to their concerns. But if there really is such a disconnect between how a mathematician thinks of her materials at a fundamental level and how it specifically gets coded up as trees in ZFC, with such huge wads of uninteresting or irrelevant stuff in its midst, we might re-examine just how appropriate ZFC is as “foundations” of our subject, or at least ask ourselves how much of it we usefully retain and how we might eliminate the dross.
We turn now to consider a categorical approach, ETCS. This will require retooling the way we think of mathematical membership. There are three respects in which “membership” or “elementhood” differs here from the way it is handled in ZFC:
- “Elements” and “sets” are entities of different types. (Meaning, elements are not themselves presupposed to be sets.)
- When we say “element”, we never mean an object considered in isolation; we always consider it relative to the specific “set” it is considered to be a member of. (That is, strictly speaking, the same object is never thought of as “belonging to” two distinct sets — use of such language must be carefully circumscribed.)
- We consider not just “elements” in the usual sense, but what are sometimes called “generalized elements”. Civilians call them “functions”. Thus, an element of type
over a domain of variation
is fancy terminology for a function
. We will call them functions or “generalized elements”, depending on the intuition we have in mind. A function
corresponds to an ordinary element of
.
Each of these corresponds to some aspect of normal practice, but taken together they are sufficiently different in how they treat “membership” that they might need some getting used to. The first corresponds to a decision to treat elements of a “set” like as ‘urelements’: they are not considered to have elements themselves and are not considered as having any internal structure; they are just atoms. What counts in a mathematical structure then is not what the constituents are ‘like’ themselves, but only how they are interrelated among themselves qua the structure they are considered being part of.
This brings us right to the second point. It corresponds e.g. to a decision never to consider a number like ‘3’ in isolation or as some Platonic essence, but always with respect to an ambient system to which it is bound, as in ‘3 qua natural number’, ‘3 qua rational number’, etc. It is a firm resolve to always honor context-dependence. Naturally, we can in a sense transport ‘3’ from one context to another via a specified function like , but strictly speaking we’ve then changed the element. This raises interesting questions, like “what if anything plays the role of extensionality?”, or “what does it mean to take the intersection of sets?”. (Globally speaking, in ETCS we don’t — but we can, with a bit of care, speak of the intersection of two “subsets” of a given set. For any real mathematical purpose, this is good enough.)
My own sense is that it may be this second precept which takes the most getting used to — it certainly gives the lie to sometimes-heard accusations that categorical set theory is just a “slavish translation of ZFC into categorical terms”. Clearly, we are witnessing here radical departure from how membership is treated in ZFC. Such unbending commitment to the principle of context-dependence might even be felt to be overkill, a perhaps pedantic exercise in austerity or purity, or that it robs us of some freedom in how we want to manipulate sets. A few quick answers: no, we don’t lose any essential freedoms. Yes, the formal language may seem slightly awkward or stilted at certain points, but the bridges between the naive and formal are mercifully fairly obvious and easily navigated. Lastly, by treating membership not as a global endo-relation on sets, but as local and relative, we effectively eliminate all the extraneous dreck and driftwood which one rightly ignores when examining the mathematics of ZFC.
The third precept is familiar from the way category theorists and logicians have used generalized elements to extend set-theoretic notation, e.g., to chase diagrams in abelian categories, or to describe sheaf semantics of intuitionistic set theory, or to flesh out the Curry-Howard isomorphism. It is a technical move in some sense, but one which is easy to grow accustomed to, and very convenient. In ETCS, there is a strong “extensionality principle” (technically, the requirement that the terminal object is a generator) which guarantees enough “ordinary” elements to make any distinctions that can sensibly be made, but experience with topos theory suggests that for many applications, it is often convenient to drop or significantly modify that principle. If anything in ETCS is a nod to traditional set theory, it is such a strong extensionality principle. [The Yoneda principle, which deals with generalized elements, is also an extensionality principle: it says that a set is determined uniquely (to within uniquely specified isomorphism) by its generalized elements.]
Okay, it is probably time to lay out the axioms of ETCS. The basic data are just those of a category; here, we are going to think of objects as “sets”, and morphisms as functions or equivalently as “elements of a set
over a domain of variation
“. The latter is a mouthful, and it is sometimes convenient to suppress explicit mention of the domain
, so that “
” just means some morphism
with codomain
. More on this below. The axioms of ETCS are the axioms of category theory, plus existence axioms which guarantee enough structure to express and support naive set theory (under the strictures imposed by precepts 1-3 above). For those who speak the lingo, the axioms below are those of a well-pointed topos with natural number object and axiom of choice. (This can be augmented later with a replacement axiom, so as to achieve bi-interpretability with full ZFC.)
Remark: As ETCS breaks the “dynamical” aspects of ZFC, and additionally treats issues of membership in a perhaps unaccustomed manner, its axioms do take longer to state. This should come as no surprise. Actually, we’ve discussed some of them already in other posts on category theory; we will repeat ourselves but make some minor adjustments to reflect normal notational practice of naive set theory, and build bridges between the naive and formal.
Axiom of products. For any two sets , there is a set
and functions
,
, such that given two elements
over the same domain, there exists a unique element
over that domain for which
A choice of product is usually denoted
. To make a bridge with naive set-theory notation, we suggestively write
where the funny equality sign and bracketing notation on the right simply mean that the cartesian product is uniquely defined up to isomorphism by its collection of (generalized) elements, which correspond to pairs of elements, in accordance with the Yoneda principle as explained in the discussion here.
We also assume the existence of an “empty product” or terminal object 1: this is a set with a unique element over any domain.
Axiom of equalizers. For any two functions , there exists a function
such that
,
- Given
over some domain such that
, there exists a unique
over the same domain such that
.
An equalizer is again defined up to isomorphism by its collection of generalized elements, denoted
, again in accordance with the Yoneda principle.
Using the last two axioms, we can form pullbacks: given functions , we can form the set denoted
using the product and equalizer indicated by this notation.
Before stating the next axiom, a few important remarks. We recall that a function is injective if for every
over the same domain,
implies
. In that case we think of
as defining a “subset”
of
, whose (generalized) elements correspond to those elements
which factor (evidently uniquely) through
. It is in that sense that we say
also “belongs to” a subset
(cf. precept 2). A relation from
to
is an injective function or subset
.
Axiom of power sets. For every set there is a choice of power set
and a relation
, so that for every relation
, there exists a unique function
such that
is obtained up to isomorphism as the pullback
In other words, belongs to
if and only if
belongs to
.
Axiom of strong extensionality. For functions , we have
if and only if
for all “ordinary” elements
.
Axiom of natural number object. There is a set , together with an element
and a function
, which is initial among sets equipped with such data. That is, given a set
together with an element
and a function
, there exists a unique function
such that
Or, in elementwise notation, for every (generalized) element
, where
means
. Under strong extensionality, we may drop the qualifier “generalized”.
Before stating the last axiom, we formulate a notion of “surjective” function: is surjective if for any two functions
, we have
if and only if
. This is dual to the notion of being injective, and under the axiom of strong extensionality, is equivalent to the familiar notion: that
is surjective if for every element
, there exists an element
such that
.
Axiom of choice. Every surjective function admits a section, i.e., a function
such that
, the identity function.
This completes the list of axioms for ETCS. I have been at pains to try to describe them in notation which is natural from the standpoint of naive set theory, with the clear implication that any formula of naive set theory is readily translated into the theory ETCS (provided we pay appropriate attention to our precepts governing membership), and that this theory provides a rigorous foundation for mainstream mathematics.
To make good on this claim, further discussion is called for. First, I have not discussed how classical first-order logic is internalized in this setting (which we would need to do justice to a comprehension or separation scheme), nor have I discussed the existence or construction of colimits. I plan to take this up later, provided I have the energy for it. Again, the plan would be to stick as closely as possible to naive set-theoretic reasoning. (This might actually be useful: the categorical treatments found in many texts tend to be technical, often involving things like monad theory and Beck’s theorem, which makes it hard for those not expert in category theory to get into. I want to show this need not be the case.)
Also, some sort of justification for the claim that ETCS “founds” mainstream mathematics is called for. Minimally, one should sketch how the reals are constructed, for instance, and one should include enough “definability theory” to make it plausible that almost all constructions in ordinary mathematics find a natural home in ETCS. What is excluded? Mainly certain parts of set theory, and parts of category theory (ha!) which involve certain parts of set theory, but this is handled by strengthening the theory with more axioms; I particularly have in mind a discussion of the replacement axiom, and perhaps large cardinal axioms. More to come!

45 comments
Comments feed for this article
September 1, 2008 at 2:36 am
John Armstrong
I haven’t had time to pore through the whole of your post, though I have a pretty good idea of where you’re heading.
One thing I want to point out is that the expectation that questions like “what is the intersection between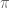 and Cantor space?” have an answer is a branch of the so-called “Cæsar problem”. The most famous, of course, is “does
and Cantor space?” have an answer is a branch of the so-called “Cæsar problem”. The most famous, of course, is “does  equal Julius Cæsar?” This is one of the problems that a structuralist approach handily knocks down.
equal Julius Cæsar?” This is one of the problems that a structuralist approach handily knocks down.
What we should say is that “set theory” is a collection of rules. A model for set theory is any collection of things (and relations between them) that satisfy these rules. No one model is any more “correct” than any other, and the Cæsar problem proceeds from trying to believe that “the” theory of sets exists.
A more real-world analogy comes from baseball teams. We can ask, “is the shortstop bald?” This or that player in the position of shortstop on this or that team may or may not be bald, but baldness is not a property of the position of shortstop itself. You can’t expect this question to have an actual answer.
September 1, 2008 at 6:43 am
Todd Trimble
We agree that no one model of a theory is more correct than another. But I wasn’t trying to pose the problem in expectation that you’d get the same answer over all models. That’s why I used the words “What in our model and implementation…”, meaning: given a model at the outset, and given a definite decision over all issues where one has to choose a convention (like ‘what is the definition of ordered pair?’, ‘are we using Cauchy’s definition of R or Dedekind’s?’, ‘which way do we take Dedekind cuts?’, etc.), then presumably there is a well-defined answer to the silly question: what is the intersection of pi and (the middle thirds) Cantor space? I even suspect some fanatic would be able to compute the answer.
Actually, I should have put it more sharply. I should have said: assuming we have introduced definitional conventions (like those listed above) where we need them, then there actually is a well-formed formula
P(x) = (x \in pi) /\ (x \in Cantor)
which one could write down in the language in ZFC, and which, given a model, would have a well-defined interpretation in that model.
My point was that ZFC contains within it not only all of mainstream mathematics, but also has huge amounts of junk we don’t want, in that it permits the formulation of well-posed questions (with well-defined answers in any given model) which “spiritually speaking” ought to be total gibberish. With the implication that in ETCS, such questions can’t even begin to be formally posed.
It’s possible that I’m not picking up on what you’re trying to say, but it looks like it might be about a different point.
September 1, 2008 at 11:43 am
James
Excellent post! Please write more of them.
September 1, 2008 at 1:14 pm
Todd Trimble
James: thanks! (Are you the James the algebraic geometer I know from the n-Category Cafe?)
When I was living in the Chicago area (1996-2000), Saunders Mac Lane floated the idea that maybe we could write a little book which would essentially be addressed at an (advanced) undergraduate level and which would present an account of categorical set theory. That never came to pass, obviously, but it means that he (who wrote a book on topos theory with Ieke Moerdijk, and a fine book it is) recognized that this approach to foundations is sophisticated, and the available accounts are largely technical and make it pretty hard for people to get into and use. And that bothered him.
I’m thinking his idea is possible, and such a book would be very useful and interesting. This post is a very preliminary dip of the toe in the water, and I would generally appreciate questions or critical feedback from readers.
September 1, 2008 at 1:49 pm
Trimble on Category Theoretic Foundations « A Dialogue on Infinity
[…] September 1, 2008 Posted by dcorfield in Uncategorized. trackback Todd Trimble has an excellent post on the Elementary Theory of the Category of Sets. He promises us more and asks for […]
September 1, 2008 at 3:12 pm
John Armstrong
I’d phrase it slightly differently. ZFC itself doesn’t contain junk, but any given model for it must necessarily contain junk. One of the structuralist points is that the only sensible questions are those which can be phrased in terms of the rules of the structure.
The rules of baseball don’t say anything about players’ hair, and so asking whether the shortstop is bald is nonsense. More seriously, there was a video of a lecture by Serre that made the rounds a year or so ago. In it, he seems to express confusion over the difference between (IIRC) the natural number and the rational number
and the rational number  , speaking as if
, speaking as if 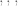 is the number
is the number  .
.
Here’s another way to put it: ZFC doesn’t permit you to pose nonsense questions. ZFC plus the choice of a model allows you to pose nonsense questions.
Similarly, it’s nonsense to ask about the sum of two points in three-dimensional affine space (even though we ask students in multivariable calculus to find such things all the time). It’s an affine space plus the choice of an origin that makes this question have an answer. But the choice of an origin would usually be arbitrary, and so the answer is rather meaningless. You can do the same sort of things with a vector space before and after you choose a basis.
As a side note: what’s fascinating is that category theory not only helps bring to the fore which questions are nonsense and which ones aren’t, but it also provides a (heuristic) language for talking about the next level up! There’s a sort of “forgetful functor” around that forgets which model of set theory we have in mind. Is there a “free” model of set theory (unique up to isomorphism of models, naturally)?
September 1, 2008 at 4:18 pm
Todd Trimble
As to the last question: there is an initial topos (with respect to logical morphisms, which preserve all topos structure), but there is no initial well-pointed or two-valued topos. [“Two-valued” here means that P(1) is isomorphic to 1 + 1 and that there are only two truth values, i.e., morphisms 1 –> 1 + 1, namely the two coproduct injections, called “false” and “true”. It may be shown that well-pointedness implies two-valuedness.]
If there were an initial two-valued topos with N, say I, then there would have to be for any two-valued topos T a logical morphism which (speaking roughly) would preserve truth values of all sentences. But we can construct a sentence in Peano arithmetic which would be true in one T, and false in another T’. So the truth value in I would have nowhere to go, so to speak. That is, initiality would force more than just one truth value; the truth value of the Peano sentence in the initial structure would lie somewhere between 0 and 1, but could collapse to 0 or 1 or somewhere in between in FP(1) when we apply a logical morphism F: I –> T, depending on the nature of T.
As for the rest: yes, it is nonsense to ask for the sum of two points in the theory of affine spaces; addition is not a definable operation in the theory. So it sounds like you’re saying that as long as a question can be expressed as a well-formed formula definable in the theory at hand (ZFC for present purposes), then we should regard it as sensible, or not nonsensical. And one *could* consistently take that point of view, and accept a wff which expresses “(x \in pi) and (x \in Cantor)” or whatever as perfectly sensible to ask, and even take well-formedness as a working definition of “sensible”.
Two reactions: (1) I don’t quite see how a sensible question under that definition becomes nonsensical when interpreted in a specific model of the theory at hand. (2) One could take that point of view on what it means to pose a sensible question, but my real point is more philosophic or intuitive: the question above is obvious gibberish at a *pre-axiomatic* level (I mean, if you were to put the question or something like it to Dedekind, he’d probably stare at you as if you were a lunatic). So it’s owing to some bizarre or let us say ‘provincial’ features of ZFC (I argue) that such a question can be given a well-defined meaning after all, and those particular bizarre features are eliminated when we pass to a theory like ETCS which exercises greater “typing discipline”.
September 1, 2008 at 5:14 pm
John Armstrong
(1) sensible questions don’t become nonsensical when you pick a model. IT’s the other way around. Given models for ZFC, for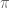 , and for Cantor space, the question is perfectly sensible. Given just the structure of ZFC the question is nonsense.
, and for Cantor space, the question is perfectly sensible. Given just the structure of ZFC the question is nonsense.
The problem arises when you assume that
(a) there is “the” [model of] set theory
(b) there is “the” construction of [a model of] the real numbers from the [model of] set theory
(c) similar to (b) but for Cantor space
But none of that exists without making arbitrary choices.
(2) The point is that we do have an intuitive meaning of what’s stuff and what’s nonsense. The philosophical question is to determine a framework that allows us to discuss set theory, and which reflects our naïve notions. My assertion is that the straight-platonism of Bourbaki ends up plagued by the Cæsar dross, but an appropriate structuralist viewpoint avoids it.
September 1, 2008 at 6:29 pm
Todd Trimble
Right, of course not. I was just drawing you out, to help clarify the public discussion.
No — that was my point. We’re not choosing a model [edit: of ZFC]. Working just in the syntax and theory of ZFC, we may embark on series of definitions leading up to a specific definition of pi, and a specific definition of Cantor space, all of which are formalizable in the language (I used the word “implementation” before, which may have been confusing — I meant *syntactic implementation* which says in effect “this is how we’re going to define the rationals in the language, the reals in the language, and so on” — in principle we could write down very complicated syntactic expressions to say what we mean).
So if we shift the question from “model” to “syntactic implementation” (of which we agree there are many choices), then I think you and I will be in perfect agreement — there is no preferred way to choose. There will be of course be further formulas to express isomorphisms between definitional choices (of say the reals). You know this, I know this, “everyone” knows this. All the same, I think there may be philosophers who insist that we make a definite choice and commit to it; has Quine for instance been observed doing that? I’m not well read in philosophy, so I’m not sure.
Anyway, the structuralist point you make is of course well known to me (but all the same I’m glad you made it). You are actually reinforcing the point of view that I’m taking, which is to avoid reifying the notion of reals (say) as defined by a definite ZFC formula, and define structures only up to isomorphism, which the categorical method does directly.
I honestly do think there is a strong tendency toward reification among committed ZFC-ists (an ordinal is…, the set of natural numbers is…, and so on); maybe they would insist this is for the sake of technical convenience, but I’m not so sure sometimes. Anyway, I’m plumping for a foundations which weaves this structuralist insight (that is part of our daily life and worldview) into the formal fabric from the get-go, rather than relegating it to a kind of meta-comment. That’s part of what is meant by bringing foundations and normal practice closer together.
Perhaps I can think of a more convincing example than pi and Cantor, though, to make my points. Thanks for the discussion.
September 1, 2008 at 8:18 pm
John Armstrong
That discussion aside, on to the pedagogy.
I’m reminded of the first two abstract algebra books I ever read. The first was a birthday present ::muffled:: years ago, simply called A First Course in Abstract Algebra. It proceeded in more or less the customary style, introducing groups, and then rings, and so on.
The second one, though, was actually much older. It was my father’s copy of Birkhoff and MacLane’s A Survey of Modern Algebra (now almost-miraculously rebound with the help of Paul Lucasiewicz, the math librarian at Yale). The thing that confounded me at first, young as I was, was that it started off with the integers, and integral domains in general. Then it moves to rational numbers and fields. It gets through polynomials, real numbers, and complex numbers before defining a group.
I’m reminded of these books because I don’t think that “the available accounts are largely technical”. The problem is that their motivating examples are split between categories like groups that students have just learned, and toy categories designed to highlight certain pathologies.
So maybe what’s called for is to start with the topos of sets, and to present it with a collection of axioms reflecting the familiar structure of naïve sets. Only later should we talk about more stripped-down examples.
Or maybe we should start with the category of (complex?) matrices, since the students should be even more consciously familiar with matrices than they are with sets. They know a lot about the valid rules for manipulating them, and they know a lot of applications for them. Here, the category theory provides the formality behind the rules for which matrices are composable.
Yes, these categories are in some sense special, and don’t reflect the variety of structures exhibited by other more general categories, but they provide a more intuitive road into the theory than starting with the most basic definitions.
September 1, 2008 at 9:01 pm
Todd Trimble
I think you misread what I was saying. By “available accounts”, I meant accounts of the development of formal categorical set theory, starting from the axioms I gave. For example, any of the topos theory books give the axioms for a topos and proceed to develop properties of a topos, giving the construction of colimits, the internal logic, Mitchell-Benabou language, and so on. That is the stuff that is generally given an efficient but highly technical account, but which in the context of ETCS I feel can be rendered in a way that many more people could understand and intuitively grok. Or so I hope.
The idea that Saunders had was to write something like “Axiomatic Categorical Set Theory”, and develop it just up to that point where people would feel comfortable translating back and forth between naive set theory and categorical set theory, and see very clearly how naive set theory receives a firm foundation in ETCS, and hopefully how natural it is. See, I think “categorical foundations” has looked hard and technical to many people who have tried to read any of the topos theory books that touch on this. That’s part of the audience “we” would be reaching out to.
If you’ve seen any of the discussions and arguments on the FOM (Foundations of Mathematics) listing from about 10 years ago, you’d see that even professional set theorists and logicians seem very confused about categorical set theory. A lot of the discussion centered on just the CST treatment of the real numbers. Basically I’d like an account which would lead up to that and only a little bit more as painlessly as possible, starting from axiomatic scratch.
A Survey of Modern Algebra, on the other hand, starts from the basics of naive set theory and develops modern algebra, gives examples, and so on. That is emphatically not the direction I had in mind for this little project — it picks up more or less where the above would leave off.
September 1, 2008 at 10:10 pm
John Armstrong
Oh, I thought you meant “available accounts” of category theory.
September 3, 2008 at 12:25 pm
James
Todd: Do you really think it’s so unlikely that you have two fans with the same first name? But you’re right. 🙂
I think your idea for a book is really good. I personally would get a lot from it. I’m pretty comfortable with toposes as categories of sheaves and as generalized topological spaces. Because of this, I think I have a decent feel for the difference between legitimate uses of sets and less legitimate ones, and so I can sense the presence of foundational issues. But my understanding of foundations is purely naive, so I can’t read the existing treatments of this stuff easily. Something for advanced undergraduates would be perfect!
Two questions:
1. It seems you’re suggesting that categories are more basic than sets. While I’m sympathetic to this, saying that 1-categories are more basic than 0-categories doesn’t seem right. Why stop at 1? Can you explain that?
2. Does ETCS give a nicer treatment of size issues in category theory? For instance presheaf categories aren’t really categories in general because the Hom sets are not sets but “large” sets. Often these problems can be solved by passing to a larger universe, but that’s ugly. Does ETCS offer a better way?
September 3, 2008 at 5:07 pm
Todd Trimble
Hi James,
“Sigh.” I just typed out a long response to your questions, and then lost it. Let me see if I can say it again (I really want to, because I think it may clarify some issues.)
To (1): since sets are conceptually simpler than categories, I consider them more basic. The question though is how one formalizes the “universe of sets” and relations between them, enough to encompass the needs of mathematicians.
In ZFC, one formalizes it as a pair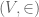 where
where  is the collection of “sets” and
is the collection of “sets” and 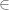 is a binary predicate on
is a binary predicate on  called the “membership” relation. Here there is no typed distinction between “sets” and “elements of sets” — everything is a set.
called the “membership” relation. Here there is no typed distinction between “sets” and “elements of sets” — everything is a set.
In ETCS, one formalizes it as a category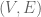 where the objects (elements of
where the objects (elements of  ) are again called “sets”, and where the morphisms (elements of
) are again called “sets”, and where the morphisms (elements of  ) are called “functions”; alternatively they are called (generalized or variable) “elements”: a function
) are called “functions”; alternatively they are called (generalized or variable) “elements”: a function 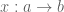 is considered “an element of
is considered “an element of 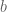 varying over a domain
varying over a domain  “. Here of course there is a typed distinction between “sets” and “elements of sets”.
“. Here of course there is a typed distinction between “sets” and “elements of sets”.
I can well see why someone might prefer ZFC over ETCS. In ZFC, we have just one type and just one predicate
and just one predicate 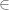 in its signature, and the first-order axioms may be expressed fairly compactly (actually, two of the “axioms” are axiom schemes, but I won’t quibble). Whereas ETCS has two types, and a number of operations in its signature (domain, codomain, composition, etc.), satisfying a number of axioms which, if one is not accustomed to universal properties and how they work, might look somewhat opaque when written out fully in the Fregean language of first-order logic, and are certainly on the longish side. (It is finitely axiomatized though.)
in its signature, and the first-order axioms may be expressed fairly compactly (actually, two of the “axioms” are axiom schemes, but I won’t quibble). Whereas ETCS has two types, and a number of operations in its signature (domain, codomain, composition, etc.), satisfying a number of axioms which, if one is not accustomed to universal properties and how they work, might look somewhat opaque when written out fully in the Fregean language of first-order logic, and are certainly on the longish side. (It is finitely axiomatized though.)
Additionally, it should be mentioned that ZFC is stronger than ETCS in that it provides for the existence of more sets, due to the separation and replacement axiom schemes (for example, in ETCS alone, one cannot form a union of iterated powers N, P(N), PP(N), … of the set of natural numbers). ETCS is bi-interpretable with a weaker theory called BZC (Bounded Zermelo with Choice), where one cuts out replacement and puts a restriction on the separation scheme. However, ETCS serves as a foundation for the mathematics in most graduate textbooks, and one can augment ETCS with a categorical replacement scheme so as to achieve a theory equivalent in power to ZFC.
In view of all this, why on earth would one prefer ETCS to ZFC? I think the answer is that, despite its apparent greater logical complexity (in part real, and in part spurious), ETCS is actually much closer to the normal practice of mathematics. In dealing with structures in normal practice, for example the ordered field of real numbers, we don’t care what the elements “are” particularly; for all intents and purposes they are just atoms, and the only important thing is how they are interrelated within the structure. In a ZFC formalization, one is committed to thinking of the elements of a structure as sets, which in turn have elements which are sets, and so on. But as mathematicians, we simply ignore the structure of the iterated membership chains as utterly irrelevant to our concerns. Then too, ZFC codings tend to inject a large degree of “ad hoc-ness” and arbitrariness; again, we shut our eyes to all that, and concentrate instead on the isomorphism-invariant properties of the abstract structure at hand. Whereas an ETCS formalization achieves all of this directly: the relevant constructions are described directly in isomorphism-invariant terms, through the use of universal properties. This brings ETCS foundations much closer to actual practice in my opinion.
As for your question (2): no I don’t think ETCS addresses set-theoretic size issues any better than ZFC. These size issues bug me a lot. I have some thoughts on this, but my thoughts are in a highly technical 2-categorical language which I don’t particularly wish to unleash on this blog; the n-Category Cafe might be a better venue for that kind of discussion. Someday, maybe.
September 3, 2008 at 11:46 pm
Sridhar
Some small technical questions: you mention adding the Axiom of Replacement to your account of ETCS (well-pointed topos with a NNO and Choice) for bi-interpretability with ZFC. What is the most appropriate way to formulate this axiom in the language of toposes? (It would not seem possible to meaningfully directly translate the normal statement of the axiom
Similarly, full Separation in ZFC allows the use of formulas with quantifiers ranging over all sets, not just bounded quantifiers, but there would not seem to be any direct translation of this into the language of toposes. In augmenting your specified structure to achieve bi-interpretability with ZFC, how does one account for this, as well? (I’m sure this is all very old hat, ho hum stuff to people in the know, but I’m not quite there yet)
September 3, 2008 at 11:47 pm
Sridhar
I don’t know what happened, but apparently my first paragraph got cut off above. Oh well; the post is still pretty coherent without the missing parts.
September 4, 2008 at 12:23 am
Todd Trimble
Sridhar, accounting for Replacement is by no means trivial. The particular account I’d like to examine more closely in connection with ETCS is one given in this nice article by Colin McLarty. As you will see, this article was written in response to some criticisms and apparent misconceptions about categorical set theory, and is one of the most clear-headed philosophic accounts I know of.
In this article, McLarty gives a proof that when ETCS is augmented by his categorical Replacement scheme, you get full bi-interpretability with ZFC (including the Separation scheme with unbounded quantifiers).
Have you taken a look at either Paul Taylor’s Practical Foundations of Mathematics or Algebraic Set Theory by Joyal and Moerdijk? They also discuss Replacement/Collection axioms (although not quite in the context of ETCS); the latter account I find a little easier to follow.
[I’ll go inside your previous comment and see if I can fix it; I have a feeling it might have been an errant < symbol which was interpreted as html.] [Edit: no, the text is missing from inside the editor’s copy too. Strange.]
September 4, 2008 at 8:19 am
James
Thanks, Todd. I think I understand what you’re saying. I think my real problem is that I don’t really even know what it means to write down *a* foundation of mathematics. It might help to see the official, formal (but hopefully not overly formal) definitions of ZFC and ETCS written side by side. Then it would probably be obvious that ETCS is an alternative to ZFC, which I accept as a foundation because people have been telling me that it works for years. And I’m not at all worried about differences in strengths–I don’t think I ever use anything outside of ETCS, which is the probably the whole reason I’m interested in this.
A few more requests, but I’d be happy to wait if they don’t fit into your expository scheme here:
1. How do you define Hom(A,B)? I’d guess this goes by looking at graphs, viewed as elements of the power set of AxB. (In fact, I should probably just do it myself…)
2. What if instead of having a power-set axiom, you had an internal-hom axiom. How would the two theories compare? I use internal homs all the time, but never look at subobject classifiers and so on, so the treatment of the subject closest to my heart might emphasize them more than power sets, but that probably says more about me than about the mathematics.
3. It would be nice to segregate the axiom of choice. Perhaps banishing AC is orthogonal to your goal, but it would be great if it’s clear exactly where AC is used and where it’s irrelevant, so those of us who don’t believe in the religion of AC can see exactly which parts are religious and which are scientific. 🙂
September 4, 2008 at 1:36 pm
Todd Trimble
Those are all good points, James, some pointing to things I was planning to take up in future posts.
There’s a decent discussion in the book by Mac Lane and Moerdijk on “categorical foundations” which compares ETCS (they call it WPT, for well-pointed topos with natural number object) with ZFC, or more exactly with a restricted form of ZFC they call RZC (restricted Zermelo with choice). What puts the “F” in ZFC is something called the replacement scheme — that’s dropped to give just ZC, and then RZC is where you place a certain technical restriction on the comprehension (aka separation) scheme. Anyway, they lay out the axioms for both theories, WPT and RZC, and show how to go back and forth between them. If you have the time and interest, you might find their discussion worthwhile.
You’ve got the right idea for defining the internal hom, or “set” hom(a, b) of all functions between two “sets” in ETCS, and you might give it a crack yourself first. Since relations 1 –> P(aXb) correspond to functions a –> P(b), you want to restrict to such functions which factor through the inclusion b –> P(b), which intuitively maps an element x in b to {x} in P(b). So along the way you need to figure out how to define this “singleton” mapping b –> P(b).
Your proposal 2. is interesting, and one could ask how much mileage you get from a finitely complete, finitely cocomplete cartesian closed category with a natural numbers object. [I’m not in this discussion considering external infinite limits/colimits, because that would presuppose a certain amount of set theory in the background, whereas what we’re considering here is a categorical “foundations” which operates autonomously, away from such background assumptions, which would feel like cheating.]
A good test case for “quasi-foundational” set-ups is: can you construct the ring of real numbers? [Also, since one would often like to be able to construct certain infinite limits and colimits, one would like to be able to “internalize” these somehow.] Looking at the first, we can certainly define the “rationals”, starting from N and applying appropriate limits and colimits. One can then try to define the reals by Cauchy’s construction (equivalence classes of certain sequences f: N –> Q, which implicitly invokes an exponential Q^N). The “certain” here involves a Cauchy condition on f, C(f), which when written out has quantifiers in it, and here we begin to see the need to interpret these quantifiers “internally”, so that you can form a subset {f in Q^N: C(f)}. Then we also need an equivalence relation on this set to express the condition that two Cauchy sequences have the same limit, and this also involves some logical quantification.
Normally, as mathematicians working at the pre-axiomatic level, we write down such sets all the time without batting an eye. In ZFC it’s an application of the “comprehension” scheme, which roughly says that given a set A and a property P written in the first-order logical theory of ZFC, you can form a set {a in A: P(a)}. In the categorical set-up, we don’t have a comprehension scheme directly; however, one can show how to build a comprehension principle from the ground up, starting with methods for internalizing first-order logic constructions. And this is where one begins to make heavy use of the subobject classifier (which turns out to be just 2=1+1 in the ETCS set-up).
So this is a big difference in style between ZFC and ETCS: in ZFC we make this huge blanket axiomatic assumption called “comprehension”, whereas ETCS starts off more parsimoniously just with the power set axiom (and the others), and shows how you get a form of comprehension anyway, enough for most mathematical purposes. Sridhar in a comment above touched on the fact that it’s not the full comprehension scheme of ZFC, but I’d rather not worry about that too much right away. Later perhaps.
As for 3.: I agree. I’m pretty “agnostic” myself on the issue of AC; . I think we all agree it’s very powerful, and a lot of mathematicians very much want all the consequences which flow from it, so I included it, but for the sake of those who feel the way you do, I’m happy to tag any result which invokes it with a label like “(AC)”. I don’t foresee any uses for quite a long time, so you are free to ignore it or set it aside until I give a heads-up. 🙂 [A little aside: Mac Lane and Moerdijk do not include this axiom in their WPT; they derive it as a consequence! But, the derivation assumes Zorn’s lemma at the metatheory level!]
September 5, 2008 at 1:11 am
Sridhar
“But, the derivation [of AC in WPT] assumes Zorn’s lemma at the metatheory level!]”. Rather like how the derivation of Booleanness in WPT assumes a classical metatheory.
Thanks for the link to the McLarty paper. Its formulation of Replacement seems pretty tied to consideration of well-pointed toposes; I wonder if something like this works more generally as well? I am thinking of how every theory extending ZF (just as in higher-order logic more generally) gives rise to a topos (objects = definable sets, morphisms = provably functional definable relations, modulo provable equivalence), though these will not generally be well-pointed. It would be nice to have a topos-theoretic formulation of Replacement encompassing these as well. [Perhaps what I am talking about is a distinction between “internal” and “external” Replacement, with the distinction collapsing, as such ones often do, in the well-pointed context]
I do indeed have a copy of Paul Taylor’s PFM which I’ve been flipping through in a slow, scattershot way. I see it discusses Replacement in the very last section; I have not yet had time to look at that in detail, but I’m sure it will throw some illumination on my thoughts. I haven’t seen Joyal and Moerdijk’s Algebraic Set Theory, but I think I’ll borrow a copy of it as well.
September 5, 2008 at 1:53 am
Todd Trimble
Sridhar — good point about Booleanness of a WPT. I myself don’t mind using classical logic at the metatheory level, even though direct proofs, when available, usually appeal to me more aesthetically. I personally don’t know of anyone who shuns classical logic at the metatheory level, although I’m sure such people exist. But I am far more ambivalent about the axiom of choice! 🙂
I can’t find my copy of Algebraic Set Theory (annoyingly enough), but from memory, they deal in a framework with a class-set distinction where the category of classes forms a pretopos, with “smallness” imposed as an extra structure. One of their axioms relating to the smallness structure is a Collection axiom. Later, they show how to construct models of intuitionistic ZF as initial algebras of a certain sort (initial as “small sup” lattices equipped with a “singleton operator”), capturing effectively in categorical form the idea of the cumulative hierarchy. Actually, they do more: depending on the properties satisfied by the singleton operator, they also show how to construct models of the class of ordinals as initial algebras, and some other things. Again, all this is in an intuitionistic setting; in particular, their Collection axiom is formulated more generally than in McLarty’s paper, so I think this should give you some idea if you can get hold of that book.
I should pause to say that I’m not an expert on this myself, but discussing it in a blog will give me an excuse to wrap my head around it! 🙂
September 5, 2008 at 3:57 am
Sridhar Ramesh
Though not particularly as an ideological decision, I do strive, as much as possible, to avoid using classical logic at the metatheory level, if only for the great applicability of the results thus obtained; even for results within the metatheory, it’s always nice to have the ability to internalize and re-use theorems in any topos of one’s choice. [Of course, one can always keep weakening one’s logic to gain even greater applicability. There is a trade-off with no particularly distinguished stopping point, but I tend to default to intuitionistic logic as a compromise position which has demonstrated its general usefulness in many ways].
None of which is to say that I feel there to be anything incorrect about classical logic [as I implied, I would be uncomfortable isolating one or another as the One True Logic], but, just as with Choice, I find it useful, or at least more “comfortable”, to keep special track of which results depend on it, with a little mental asterisk.
September 5, 2008 at 4:03 am
Todd Trimble
Sridhar — well said!
September 7, 2008 at 7:23 am
James
Thanks, Todd.
I had a look at Mac Lane-Moerdijk. I think my problem is that you and they don’t write down the preamble to the axioms. It seems kind of like writing down just the group axioms but skipping the part that goes “A group is a set with a binary operation such that”. I’d guess the reason is that the preamble for ZFC or ETCS would be something purely syntactic involving words like “symbol” and “alphabet” which would be painful to write and read. Is that true? Nevertheless, at some point (in this series of posts I hope you’ll write) I would like to see the preamble, if there is one.
September 7, 2008 at 4:12 pm
Todd Trimble
James — I really hope I understand what you’re saying or asking. But let me know if I’ve missed the mark.
As you know, what mathematicians usually do when they define concepts, say the notion of group, is to proceed in the way you suggested: a group is a set equipped with some operations satisfying blah blah blah. Logicians or model theorists, who need to distinguish between theories and models, might proceed for their purposes in more official-sounding or perhaps more pedantic-sounding terms, saying something like: “The theory of groups is a one-sorted first-order theory of signature [m, i, e] where m is a binary function symbol, i [inversion] is an unary function symbol, and e is a constant, satisfying the following axioms
forall x, y, z: m(m(x, y), z) = m(x, m(y, z))
[and so on]. A group is a model of the theory of groups.”
To describe ETCS, I prefer to sound more like a ordinary mathematician at first. That is, I would first describe what are actually the models of ETCS: as, e.g., well-pointed toposes with natural numbers and choice. For people comfortable with category-speak, these are categories with finite products, equalizers, power objects, a natural numbers object, in which the terminal object is a generator, and in which every epimorphism splits [has a section].
Then, taking this as scaffold, we could then write out in traditional formal logic terms the actual full-fledged formal theory ETCS. My gut instinct is to rely on readers’ good will that there is no difficulty in principle in going about this, although it’s somewhat tedious. In one formulation it might go like this: the theory ETCS has
Three sort symbols: C_0, C_1, C_2 [representing the classes of objects, morphisms, and composable pairs of morphisms],
Function symbols [corresponding to the idea that a category is a truncated simplicial set]:
d_10: C_1 –> C_0, d_11: C_1 –> C_0,
s_00: C_0 –> C_1,
d_20: C_2 –> C_1, d_21: C_2 –> C_1, d_22: C_2 –> C_1
s_10: C_1 –> C_2, s_11: C_1 –> C_2
satisfying a bunch of equational axioms which we could write out in first-order logic terms, including simplicial identities, identities implying C_2 with its projections d_20, d_22 is a pullback of d_10 against d_11 [so that C_2 really does represent the class of composable pairs], associativity and identity axioms for categories, and then six more gotten by transcribing the axioms I described in my post into formal logical terms involving this data.
And yes, it would obviously be painful to spell it out in these terms!
Professional ZFC-ists hostile to categorical foundations seem to love pointing out this fact. I suppose this could be considered devastating criticism if humans understood mathematics primarily in such heavy formal terms, instead of being able to clearly grasp conceptual gestalts. Anyway, in the interest of full disclosure, that is how the theory ETCS might be described in the traditional terms of formal first-order logic. I’m not quite sure that’s what you’re after, but there it is.
[I will remark, for any such professional set-theorists who happen to be reading this, that the notion of a category with specified finite limits, power objects and natural numbers object (that is, a topos with N) is one expressible in equational Horn logic; in other words, one which can be internalized in any category with finite limits. This would correspond to, or be bi-interpretable with, intuitionistic bounded Zermelo set theory.]
The story with ZFC is a little different — here it doesn’t make much sense to try to say what the models are precisely before we actually lay out the formal theory, because the list of ZFC axioms is in fact infinite; to encompass it using finitely many syllables, we need recourse to axiom schemes (comprehension or separation, replacement) which refer to classes of formulas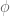 which can be built up in the formal language. Without trying to be too precise, we can say that a ZFC structure consists of a universe (a collection, or “set” if you like) V and a binary relation
which can be built up in the formal language. Without trying to be too precise, we can say that a ZFC structure consists of a universe (a collection, or “set” if you like) V and a binary relation 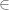 on V, and this data is then subject to a big bunch of ZFC axioms.
on V, and this data is then subject to a big bunch of ZFC axioms.
But really, what I’m after is this: try to indicate or sketch, gradually, that all of “ordinary mathematics” can be “internalized” within a well-pointed topos with natural numbers and choice. In my upcoming post on this, I will begin by showing how (at least some; it will take more than one post to get all) the usual logical operations find a home — can be internalized — within such a category. Then I will begin to get other useful constructions, like finite colimits, and also more general internal limits and colimits over definable diagrams. Then I will show how to internalize the real numbers. It all builds from there. When I say that ETCS is a “foundations for ordinary mathematics”, I really just mean that all “ordinary” mathematical constructions can be interpreted within a WPT + N + C, and all “ordinary” theorems can be proved in the internal logic of such a category. I hope this makes some sense!
September 7, 2008 at 8:44 pm
Sridhar Ramesh
If the “preamble” to the group axioms is just “A group is a collection with a binary connective such that…”, then the appropriate “preamble” for ETCS would seem to be just the same as for the category axioms (which I’m sure you have in some older post; something like “A category is a collection of objects, any ordered pair of which is associated with a collection of morphisms, and a composition operator on certain sequences of morphisms such that…”). The issue of translation into particular conventional low-level formal logical systems would appear to be a separate one.
September 8, 2008 at 12:46 pm
James
Thanks Todd and Sridhar. Things are getting clearer, but rather than continuing to ask questions, I think I’ll just stop for a bit and watch things unfold. I’ll probably come back with some more later.
September 10, 2008 at 11:57 pm
ETCS: Internalizing the logic « Todd and Vishal’s blog
[…] of “the elementary theory of the category of sets” [ETCS] which we had begun last time, here and in the comments which followed. My thanks go to all who commented, for some useful feedback and […]
November 22, 2008 at 10:20 am
James
Hi Todd. I just read some of the recent Notices issue on automated proof checkers. Has anyone written one based on ETCS? I think once someone does this, it would be impossible to have a philosophical objection to using topos theory as a foundation.
November 26, 2008 at 12:07 pm
Todd Trimble
Hi James,
Thanks for bringing this number of the Notices to my attention (and sorry for the delay in responding — I’ve unfortunately been very busy with other stuff). I’m not positive yet which of those articles caught your eye, but I’m going to guess that it was the one by Georges Gonthier on computer formalization of the proof of the Four Color Theorem.
In the section on the calculus of dependent types (“Coq and the Calculus of Inductive Constructions”), Gonthier makes some very good points that relate directly to a crucial philosophic difference between ZFC and ETCS. We may as well take his first example, commutativity of addition of natural numbers:
In ZFC, where variables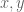 do not already have types assigned to them, one has to express the universal quantifier by a circumlocution like
do not already have types assigned to them, one has to express the universal quantifier by a circumlocution like
where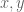 are variables whose values range over sets (“if the sets
are variables whose values range over sets (“if the sets  and
and  happen to be natural numbers, then their sums taken in either order agree”). Logically, there is nothing wrong with this, but the expression as it stands is a little weird, since
happen to be natural numbers, then their sums taken in either order agree”). Logically, there is nothing wrong with this, but the expression as it stands is a little weird, since 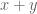 has no sense to it if
has no sense to it if 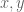 are general free-floating sets. As Gonthier says, the premises [of membership in
are general free-floating sets. As Gonthier says, the premises [of membership in  ] have to be checked each time the law of commutativity is to be applied, and in a fully formalized proof, where the terms for
] have to be checked each time the law of commutativity is to be applied, and in a fully formalized proof, where the terms for  and
and  may be complicated, this may actually turn out to be a bigger deal than one might at first suspect.
may be complicated, this may actually turn out to be a bigger deal than one might at first suspect.
In ETCS this doesn’t come up, because “membership” there doesn’t work that way, i.e., is not a global relation between free-floating sets. Rather, ETCS is a typed theory, i.e., elements in ETCS have preassigned types to which they belong [recall that I wrote “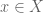 ” to mean
” to mean  is a morphism with codomain
is a morphism with codomain  : morphisms have domains and codomains assigned to them]. Most people working with typed theories don’t even use the membership symbol, possibly because it gives rise to misleading associations with traditional (non-typed) set theory. But anyway, in a fully formalized computer proof, there will be type-checking protocols in place every step of the way, so that one can’t even write expressions like
: morphisms have domains and codomains assigned to them]. Most people working with typed theories don’t even use the membership symbol, possibly because it gives rise to misleading associations with traditional (non-typed) set theory. But anyway, in a fully formalized computer proof, there will be type-checking protocols in place every step of the way, so that one can’t even write expressions like 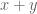 unless
unless 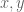 are terms of the same type; otherwise a loud buzzer sounds off and the message “type error” appears.
are terms of the same type; otherwise a loud buzzer sounds off and the message “type error” appears.
So, in answer to your question, as a matter of course people do use typed theories in sophisticated systems like “Coq”, not always with the full topos-theoretic power of ETCS, but that’s exactly the kind of theory these systems would be based on (and as a matter of fact category theory, specifically locally cartesian closed categories of which toposes are primary examples, have been instrumental in laying down the semantics foundations of the calculus of dependent types that Gonthier discusses). So great, I’m glad he made those points, and indeed ETCS, not ZFC, is the right kind of set theory for computerized mathematics in the 21st century!
November 26, 2008 at 6:16 pm
Mathieu Dupont
I use myself “:” to declare the type of a variable instead of “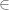 ”. The reason is that the symbol “
”. The reason is that the symbol “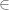 ” has another meaning in mathematics: it denotes the membership relation between elements of a set and subsets of the same set. So I can write “
” has another meaning in mathematics: it denotes the membership relation between elements of a set and subsets of the same set. So I can write “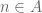 ”, if
”, if 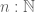 and
and 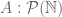 . In the same context, by a slight abuse of notation, we can write “let
. In the same context, by a slight abuse of notation, we can write “let 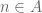 ” instead of “let
” instead of “let 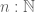 such that
such that 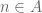 ”.
”.
These are very different ideas and they need different symbols: on the one hand we have a syntactical relation between symbols and on the other hand a mathematical relation between mathematical objects. The confusion comes from the more or less explicit assumption in ZF or similar theories of a universal set of which each set is a subset, so that there is only one type and by the abuse of notation mentioned above, for a set
and by the abuse of notation mentioned above, for a set  , we can write simply “let
, we can write simply “let  ” instead of “let
” instead of “let  such that
such that  ”.
”.
November 26, 2008 at 8:55 pm
Todd Trimble
Mathieu: you’re right, and elsewhere I often use the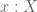 notation myself. I chose not to in the series of posts so far, just because many people are not familiar with that notation. In one of my posts, I used “is in” to denote the membership relation between an element of a set and a subset of that set (in other words, I agree with you that the concepts are different and require different notation). Perhaps one could argue that I should be less idiosyncratic, and use the standard notation you just mentioned, but life is full of funny choices, isn’t it? 🙂
notation myself. I chose not to in the series of posts so far, just because many people are not familiar with that notation. In one of my posts, I used “is in” to denote the membership relation between an element of a set and a subset of that set (in other words, I agree with you that the concepts are different and require different notation). Perhaps one could argue that I should be less idiosyncratic, and use the standard notation you just mentioned, but life is full of funny choices, isn’t it? 🙂
November 30, 2008 at 12:13 am
James
Thanks, Todd. Really, all the articles on formal proof caught my eye. I still wasn’t happy with my understanding of what it means to have _a_ foundation of mathematics. I mean, how do you define ‘topos’ without knowing what ‘category’ means, and how do you define ‘category’ without knowing what ‘set’ means? And all this business about meta-language obscured things further. But when reading those articles in the Notices, I thought that it’s probably reasonable to say you have a foundation of mathematics if and only if you can write an automated proof checker based on it. (Whether it’s powerful enough to serve as a foundation for every subject that calls itself mathematics is another question.)
November 30, 2008 at 1:24 am
Todd Trimble
These questions seem to me close in spirit to some questions Urs Schreiber has been asking over at the -Category Café, in the comments following the post “Coalgebraically Thinking”, starting about here. Don’t know whether you’ve been following that thread, but I thought you might find some of the discussion interesting [edit: oh, I see you have been following this!]. Toby Bartels has been making some very pertinent points in response, and I would strongly recommend to anyone grappling with these issues to take his points to heart.
-Category Café, in the comments following the post “Coalgebraically Thinking”, starting about here. Don’t know whether you’ve been following that thread, but I thought you might find some of the discussion interesting [edit: oh, I see you have been following this!]. Toby Bartels has been making some very pertinent points in response, and I would strongly recommend to anyone grappling with these issues to take his points to heart.
I think one important point is that even though everyone thinks they know what sets “are”, sets are never defined. Thus the purpose of an axiomatization, that is, a “set theory”, is not so much to describe what sets are, but to give a language rich enough to express any conceivable use that “sets” might be put to in mathematics. (One should note well that the language, the syntax itself, does not invoke the word “set” at all, even though the intended semantics may be all about constructing complicated collections to express mathematical ideas.)
You are right: conceptually, ‘category’ is prior to ‘topos’ [you can’t say what a topos is without using the word ‘category’], and categories are sets which comes equipped with extra structure satisfying certain properties. Conceptually, nothing is more basic than the idea of ‘set’ or ‘collection’. Still, the real issue in set-theoretic “foundations” [whether ZF or ETCS or whatever] is again not what sets “are”, but what sorts of operations or constructions on sets will we need to get mathematics off the ground, and how do we express them logically, efficiently, usefully, insightfully? Category theory is used here by no means to suggest that categories are conceptually more basic than sets, but rather to organize and to shed light on the nature of set-theoretic constructions, and on the structure of mathematical logic itself.
The backdrop of any of these foundational theories, the sine qua non, is first-order logic, and you could say that these theories, aside from any semantic content, are nothing more than languages written in first-order logic with some extra-logical symbols (e.g.,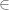 in ZF), and the precise rules for inferring theorems from axioms. Therefore, yes: if one fully mechanizes the description of such a language, and has strong empirical evidence that the corpus of mathematical literature is encodable or expressible in such a language, then that’s what we should mean by foundations. I think that’s quite close, perhaps identical, to what you were proposing with automated proof checkers, and in that sense we are probably in agreement.
in ZF), and the precise rules for inferring theorems from axioms. Therefore, yes: if one fully mechanizes the description of such a language, and has strong empirical evidence that the corpus of mathematical literature is encodable or expressible in such a language, then that’s what we should mean by foundations. I think that’s quite close, perhaps identical, to what you were proposing with automated proof checkers, and in that sense we are probably in agreement.
December 7, 2008 at 10:49 am
Can Category Theory Serve as the Foundation of Mathematics? « Combinatorics and more
[…] and Vishal Blog) a series of posts ( I, II, III) on category theory, and additional posts (I,II) on category theory and axiomatic set theory. See also the remark below. Possibly related […]
December 15, 2008 at 12:54 pm
ETCS: Building joins and coproducts « Todd and Vishal’s blog
[…] philosophy for now; readers may refer to my earlier posts for more. Let’s get to work, shall we? Our last post was about the structure of (and […]
March 3, 2009 at 4:05 pm
Higher-dimensional order theory » The two meanings of the word “set” in mathematics
[…] Sets for mathematics by Lawvere and Rosebrugh, or Todd Trimble’s posts on his blog about the Elementary Theory of the Category of Sets for a semi-elementary approach to toposes. Note that, in a topos, for each object , there is an […]
March 6, 2009 at 12:49 am
slawekk
x + y has no sense to it if x, y are general free-floating sets
In ZF implementations if x is not in the domain of a function f, then f(x) evaluates to the empty set. In Isabelle/ZF this is lemma apply_0 in func.thy theory file and in Metamath see Theorem ndmfv.
the premises [of membership in \mathbb{N}] have to be checked each time the law of commutativity is to be applied, and in a fully formalized proof, where the terms for x and y may be complicated, this may actually turn out to be a bigger deal than one might at first suspect.
Yes, it adds about 10% to the formalization effort. However, I don’t think any type theory helps here much, except for the simplest cases. Consider something like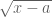 . You can not express
. You can not express 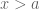 in simple type theory where the inference is automatic, you need to provide a proof. For dependent type theory inference may not be automatic and again you need to provide a proof.
in simple type theory where the inference is automatic, you need to provide a proof. For dependent type theory inference may not be automatic and again you need to provide a proof.
as a matter of course people do use typed theories in sophisticated systems like “Coq”
People use type theory in systems whose primary design goal is software verification, like COQ, Isabelle/HOL or HOL Light. It is a matter of taste which foundation is “better” but it is good to remember that there are systems like Mizar, Metamath and Isabelle/ZF that implement ZF set theory.
As for James’ question Freek Wiedijk mentions an attempt to write down the axioms of category theory in a formal proof language in his “Is ZF a hack”.
March 7, 2009 at 3:53 pm
Todd Trimble
slawekk, I’m not knowledgeable about programming language design, so I can’t speak to 10% statistic nor to the languages you mention such as Mizar. But it may also be good to keep in mind that the axioms I’ve been discussing in ETCS, together with a few others, express the same mathematical content as ZF, in that this augmented language ETCS+ and ZF are interpretable in one another. Thus one could say that ETCS+ implements ZF.
The question becomes what presentation of set theory is best suited for a particular range of applications.
As for the rest, perhaps your objections are better directed to Gonthier, not me. As I say, I don’t claim to know much about programming languages.
March 7, 2009 at 8:05 pm
slawekk
Just to clarify, my comment was not related to programming language design. It was about formal proof languages, i.e. languages you can use to write (formal) proofs. It was also a bit about relative merits of ZF set theory vs. typed theories (like ETCS) as foundations for “computerized mathematics in the 21st century”.
10% statistics was about “formalization effort”. It meant that when you write a (formal) proof in ZF set theory about 10% of work goes into justifying set membership so that one can use laws like commutativity.
Mizar is the name of a formal proof language and verifier with the most extensive library of proofs. The Mizar system is based on Tarski–Grothendieck set theory.
I think discussions about ETCS would be much more interesting if one could see its axioms and some definitions and theorems written in a formal proof language. I agree with James that “once someone does this, it would be impossible to have a philosophical objection to using topos theory as a foundation”.
March 7, 2009 at 10:30 pm
Todd Trimble
slawekk wrote:
Naturally, what is interesting is a matter of taste. Ultimately I think that would be a worthwhile thing to pursue, but I don’t plan on doing that here in this blog. I plan to continue this discussion as I have already, in a more traditional format of mathematical discourse.
September 5, 2013 at 1:16 pm
Bernardo
This post is really a pleasant one it helps new web users, who
are wishing for blogging.
March 30, 2015 at 6:04 pm
Leone Partlow
Top site, a bientot sur la toile
September 29, 2015 at 3:42 pm
Ali Sadegh Daghighi
Dear Todd,
This is a very interesting discussion which points out to a classic battle between set theorists and category theorists.
But maybe because of not too good formatting of the blog pages (particularly in the comment part) following the discussions is a bit hard (at least for me).
It will be perfect if you improve the appearance of your blog, say by enlarging the font and expanding the width of the text containing parts which makes the vertical length of the posts shorter as well as decreasing the need for scrolling.
Good Luck
July 24, 2018 at 4:57 am
ZFC and ETCS: Elementary Theory of the Category of Sets. "A lot of confusion seems to reign around 'the categorical approach to foundations' and what it might entail" - Nevin Manimala's Blog
[…] by /u/flexibeast [link] […]